Nomor 21
Seutas tali dipotong menjasi 6 bagian sehingga potongan-potongan tersebut membentuk deret geometri. Jika tali terpendek 5 cm dan tali terplanjang
160 cm, panjang tali tersebut sebelum dipotong adalah ...
♠ Barisan geometri : un=arn−1 dan sn=a(rn−1)r−1
Diketahui a=5,u6=160,n=6
u6=160⇔ar5=160⇔5r5=160⇔r=2
♠ Menentukan panjang total talinya (s6) :
sn=a(rn−1)r−1s6=5(26−1)2−1=5.36=315
Jadi, panjang tali sebelumnya adalah 315 cm .♡
Diketahui a=5,u6=160,n=6
u6=160⇔ar5=160⇔5r5=160⇔r=2
♠ Menentukan panjang total talinya (s6) :
sn=a(rn−1)r−1s6=5(26−1)2−1=5.36=315
Jadi, panjang tali sebelumnya adalah 315 cm .♡
Nomor 22
Diketahui balok KLMN.PQRS dengan KL = 3 cm , LM = 4 cm, dan KP = 12 cm. Jarak titik R ke garis PM adalah ....
♣ Gambar balok dan segitiganya :

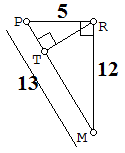
♣ Gunakan luas segitiga PMR :
LΔPMR=LΔPMR12.PM.TR=12.RM.RP(coret 12)PM.TR=RM.RP13.TR=12.5TR=6013
Jadi, panjang TR=6013 cm. ♡


♣ Gunakan luas segitiga PMR :
LΔPMR=LΔPMR12.PM.TR=12.RM.RP(coret 12)PM.TR=RM.RP13.TR=12.5TR=6013
Jadi, panjang TR=6013 cm. ♡
Nomor 23
Kubus ABCD.EFGH memiliki rusuk 4 cm. Sudut antara AE dan bidang AFH adalah α . Nilai sinα=...
♠ Gambar balok dan segitiganya :


♠ Menentukan sinus sudutnya :
∠(EA,ΔAFH)=∠(AE,AP)=θ
sinθ=EPAP=2√22√6=√2√6.√6√6=√126=2√36sinθ=√33=13√3
Jadi, nilai sinθ=13√3.♡


♠ Menentukan sinus sudutnya :
∠(EA,ΔAFH)=∠(AE,AP)=θ
sinθ=EPAP=2√22√6=√2√6.√6√6=√126=2√36sinθ=√33=13√3
Jadi, nilai sinθ=13√3.♡
Nomor 24
Diketahui jajargenjang seperti gambar.
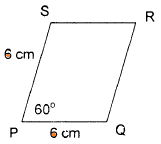
Panjang diagonal PR = ...

Panjang diagonal PR = ...
Cara I :
♣ Gambar lengkapnya :
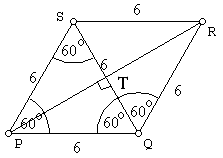
♣ Aturan cosinus pada sisi PR :
PR2=QP2+QR2−2.QP.QR.cosPQR=62+62−2.6.6.cos120o=36+36−72.(−12)=72+36PR2=108PR=√108=6√3
Jadi, panjang PR=6√3.♡
♣ Gambar lengkapnya :

♣ Aturan cosinus pada sisi PR :
PR2=QP2+QR2−2.QP.QR.cosPQR=62+62−2.6.6.cos120o=36+36−72.(−12)=72+36PR2=108PR=√108=6√3
Jadi, panjang PR=6√3.♡
Cara II :
♣ Gambar lengkapnya :

♣ Perhatikan segitiga PQT :
sinQ=PTPQsin60o=PT612√3=PT6PT=6.12√3PT=3√3
Jadi, panjang PR=2.PT=2×3√3=6√3.♡
♣ Gambar lengkapnya :

♣ Perhatikan segitiga PQT :
sinQ=PTPQsin60o=PT612√3=PT6PT=6.12√3PT=3√3
Jadi, panjang PR=2.PT=2×3√3=6√3.♡
Cara III :
♣ Gambar lengkapnya :

♣ Perhatikan segitiga PQT , QT=12QS=3 dan gunakan pythagoras:
PT=√PQ2−QT2=√62−32=√36−9=√27PT=3√3
Jadi, panjang PR=2.PT=2×3√3=6√3.♡
♣ Gambar lengkapnya :

♣ Perhatikan segitiga PQT , QT=12QS=3 dan gunakan pythagoras:
PT=√PQ2−QT2=√62−32=√36−9=√27PT=3√3
Jadi, panjang PR=2.PT=2×3√3=6√3.♡
Nomor 25
Himpunan penyelesaian dari persamaan 2cos2x+5sinx−4=0 untuk 0o≤x≤360o adalah ...
♠ Misalkan p=sinx dan gunakan sin2x+cos2x=1 :
2cos2x+5sinx−4=02(1−sin2x)+5sinx−4=02−2sin2x+5sinx−4=02sin2x−5sinx+2=02p2−5p+2=0(2p−1)(p−2)=0p=12ataup=2p=12⇒sinx=12⇒x={30o,150o}p=2⇒sinx=2(tidak ada nilaix yang memenuhi )(nilai maksimum darisinxadalah 1)
Jadi, HP={30o,150o}.♡
2cos2x+5sinx−4=02(1−sin2x)+5sinx−4=02−2sin2x+5sinx−4=02sin2x−5sinx+2=02p2−5p+2=0(2p−1)(p−2)=0p=12ataup=2p=12⇒sinx=12⇒x={30o,150o}p=2⇒sinx=2(tidak ada nilaix yang memenuhi )(nilai maksimum darisinxadalah 1)
Jadi, HP={30o,150o}.♡


Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.