Nomor 1
Jika salah satu akar dari persamaan kuadrat x2−4(k+1)x+k2−k+7=0 bernilai tiga kali dari akar yang lain dan semua akar-akar bernilai
lebih dari 2, maka himpunan semua bilangan k yang memenuhi adalah ...
♣ PK x2−4(k+1)x+k2−k+7=0 akar - akarnya x1 dan x2
x1+x2=−ba=−[−4(k+1)]1=4(k+1)
artinya x1+x2=4(k+1) ...pers(i)
♣ Salah satu akarnya bernilai tiga kali akar yang lainnya
x1=3x2 ....pers(ii)
♣ Substitusi x1=3x2 ke pers(i)
x1+x2=4(k+1)→3x2+x2=4(k+1)→x2=k+1
♣ Substitusi x2=k+1 ke PK
x2−4(k+1)x+k2−k+7=0(k+1)2−4(k+1)(k+1)+k2−k+7=02k2+7k−4=0(2k−1)(k+4)=0k=12∨k=−4
♣ Semua akar-akarnya lebih dari 2
x1>2 dan x2>2Jumlahkan keduanya x1+x2>2+2x1+x2>44(k+1)>4k+1>1k>0
Karena nilai k>0 , maka yang memenuhi adalah k=12
Jadi, nilai k yang memenuhi adalah k=12.♡
x1+x2=−ba=−[−4(k+1)]1=4(k+1)
artinya x1+x2=4(k+1) ...pers(i)
♣ Salah satu akarnya bernilai tiga kali akar yang lainnya
x1=3x2 ....pers(ii)
♣ Substitusi x1=3x2 ke pers(i)
x1+x2=4(k+1)→3x2+x2=4(k+1)→x2=k+1
♣ Substitusi x2=k+1 ke PK
x2−4(k+1)x+k2−k+7=0(k+1)2−4(k+1)(k+1)+k2−k+7=02k2+7k−4=0(2k−1)(k+4)=0k=12∨k=−4
♣ Semua akar-akarnya lebih dari 2
x1>2 dan x2>2Jumlahkan keduanya x1+x2>2+2x1+x2>44(k+1)>4k+1>1k>0
Karena nilai k>0 , maka yang memenuhi adalah k=12
Jadi, nilai k yang memenuhi adalah k=12.♡
Nomor 2
Diketahui f(x)=x2−4g(x)+3,h(x)=g(x)+3x+1,
m(x)=h(x)−2x−1;x≠1;m(1)=2014.
Jika f(x) dibagi x2+x−2 memiliki sisa ax+b , maka nilai a+2b=...
m(x)=h(x)−2x−1;x≠1;m(1)=2014.
Jika f(x) dibagi x2+x−2 memiliki sisa ax+b , maka nilai a+2b=...
♠ Nilai m(1)=2014 (untuk x=1) dan m(x)=h(x)−2x−1 tidak boleh untuk x=1
, maka haruslah h(x)−2 memeiliki faktor (x−1), sehingga
h(x)−2=(x−1).k(x)h(x)=(x−1).k(x)+2....pers(i)
dengan k(x) suatu fungsi tertentu (polinomial)
♠ Substitusi x=1 ke pers(i)
x=1→h(x)=(x−1).k(x)+2h(1)=(1−1).k(1)+2h(1)=2
♠ Substitusi x=1 dan h(1)=2
x=1→h(x)=g(x)+3x+1h(1)=g(1)+31+12=g(1)+32g(1)=1
♠ Substitusi x=1 dan g(1)=1
x=1→f(x)=x2−4g(x)+3f(1)=12−4g(1)+3f(1)=−3g(1)+3f(1)=0
♠ Substitusi x=−2
x=−2→f(x)=x2−4g(x)+3f(−2)=(−2)2−4g(−2)+3f(−2)=4−4g(−2)+3f(−2)=3
Diperoleh f(1)=0 dan f(−2)=3
♠ Fungsi f(x) dibagi x2+x−2 sisanya ax+b dan anggap hasilnya z(x) , dapat ditulis
f(x)=(x2+x−2).z(x)+(ax+b) ....pers(ii)
atau f(x)=(x−1)(x+2).z(x)+(ax+b) ....pers(ii)
♠ Substitusi x=1 dan x=−2 ke pers(ii)
x=1→f(x)=(x−1)(x+2).z(x)+(ax+b)f(1)=(1−1)(1+2).z(1)+(a.1+b)0=a+b...pers(iii)x=−2→f(x)=(x−1)(x+2).z(x)+(ax+b)f(−2)=(−2−1)(−2+2).z(−2)+(a.(−2)+b)3=−2a+b...pers(iv)
♠ Eliminasi pers(iii) dan pers(iv)
a+b=0−2a+b=3−3a=−3a=−1
pers(iii) : a+b=0→−1+b=0→b=1
Sehingga nilai a+2b=−1+2.1=−1+2=1
Jadi, nilai a+2b=1.♡
h(x)−2=(x−1).k(x)h(x)=(x−1).k(x)+2....pers(i)
dengan k(x) suatu fungsi tertentu (polinomial)
♠ Substitusi x=1 ke pers(i)
x=1→h(x)=(x−1).k(x)+2h(1)=(1−1).k(1)+2h(1)=2
♠ Substitusi x=1 dan h(1)=2
x=1→h(x)=g(x)+3x+1h(1)=g(1)+31+12=g(1)+32g(1)=1
♠ Substitusi x=1 dan g(1)=1
x=1→f(x)=x2−4g(x)+3f(1)=12−4g(1)+3f(1)=−3g(1)+3f(1)=0
♠ Substitusi x=−2
x=−2→f(x)=x2−4g(x)+3f(−2)=(−2)2−4g(−2)+3f(−2)=4−4g(−2)+3f(−2)=3
Diperoleh f(1)=0 dan f(−2)=3
♠ Fungsi f(x) dibagi x2+x−2 sisanya ax+b dan anggap hasilnya z(x) , dapat ditulis
f(x)=(x2+x−2).z(x)+(ax+b) ....pers(ii)
atau f(x)=(x−1)(x+2).z(x)+(ax+b) ....pers(ii)
♠ Substitusi x=1 dan x=−2 ke pers(ii)
x=1→f(x)=(x−1)(x+2).z(x)+(ax+b)f(1)=(1−1)(1+2).z(1)+(a.1+b)0=a+b...pers(iii)x=−2→f(x)=(x−1)(x+2).z(x)+(ax+b)f(−2)=(−2−1)(−2+2).z(−2)+(a.(−2)+b)3=−2a+b...pers(iv)
♠ Eliminasi pers(iii) dan pers(iv)
a+b=0−2a+b=3−3a=−3a=−1
pers(iii) : a+b=0→−1+b=0→b=1
Sehingga nilai a+2b=−1+2.1=−1+2=1
Jadi, nilai a+2b=1.♡
Nomor 3
Himpunan semua bilangan x yang memenuhi pertidaksamaan 1√x+1−√x≤√2x+5 adalah ...
♣ Karena nilai √x+1 tidak akan sama dengan nilai √x (dua bilangan berurutan tidak akan pernah
sama nilainya), maka pasti nilai √x+1−√x≠0 , sehingga bisa dirasionalkan bentuk pecahannya dan tidak akan
mengurangi akar-akarnya karena penyebutnya yang hilang.
♣ Rasionalkan ruas kiri
1√x+1−√x≤√2x+51√x+1−√x.√x+1+√x√x+1+√x≤√2x+5√x+1+√x(x+1)−(x)≤√2x+5√x+1+√x≤√2x+5
♣ Kuadratkan kedua ruas
(√x+1+√x)2≤(√2x+5)2(x+1)+x+2√x2+x≤2x+5√x2+x≤2(kuadratkan lagi)x2+x≤4x2+x−4≤0x1,2=−1±√172

HP1 = {−1−√172≤x≤−1+√172}
♣ Menentukan syarat-syarat akar
*). √x+1 syaratnya : x+1≥0→x≥−1
*). √x syaratnya : x≥0
*). √2x+5 syaratnya : 2x+5≥0→x≥−52
Syarat yang memenuhi ketiganya adalah : HP2 = {x≥0}
Sehingga solusinya : HP = HP1 ∩ HP2 = {0≤x≤−1+√172}
Jadi, solusinya HP = {0≤x≤−1+√172}.♡
♣ Rasionalkan ruas kiri
1√x+1−√x≤√2x+51√x+1−√x.√x+1+√x√x+1+√x≤√2x+5√x+1+√x(x+1)−(x)≤√2x+5√x+1+√x≤√2x+5
♣ Kuadratkan kedua ruas
(√x+1+√x)2≤(√2x+5)2(x+1)+x+2√x2+x≤2x+5√x2+x≤2(kuadratkan lagi)x2+x≤4x2+x−4≤0x1,2=−1±√172

HP1 = {−1−√172≤x≤−1+√172}
♣ Menentukan syarat-syarat akar
*). √x+1 syaratnya : x+1≥0→x≥−1
*). √x syaratnya : x≥0
*). √2x+5 syaratnya : 2x+5≥0→x≥−52
Syarat yang memenuhi ketiganya adalah : HP2 = {x≥0}
Sehingga solusinya : HP = HP1 ∩ HP2 = {0≤x≤−1+√172}
Jadi, solusinya HP = {0≤x≤−1+√172}.♡
Nomor 4
A dan B berdiri saling berhadapan dengan jarak 100 m. Seekor kucing bediri di samping A dan mulai berlari menuju B dengan kecepatan 2 m/s.
Pada saat yang sama, A berjalan menuju B dengan kecepatan 1 m/s dan berhenti ketika kucing tiba di B. Kucing lalu berbalik arah dan berlari menuju A
dengan kecepatan yang sama. B tidak bergerak dari posisi awal. Kemudian, kucing dan A kembali menuju B dengan kecepatannya masing-masing. Jika proses ini
berlanjut terus-menerus, jarak yang ditempuh oleh kucing adalah ... m.
♠ Konsep geometri tak hingga : S∞=a1−r
♠ Misal, Misal SA = jarak A yang ditempuh
dan Sk = jarak kucing yang ditempuh.
Rumus jarak : S=V.t dengan V jarak dan t adalah waktu.
Vk=2 m/s dan VA=1 m/s , artinya jarak yang ditempuh oleh A separuh dari jarak yang ditempuh oleh kucing. Berikut ilustrasi pergerakan kucing dan A .

♠ Menentukan total jarak yang ditempuh kucing
Dari ilustrasi gambar di atas, jarak total yang ditempuh kucing : Sk=100+50+50+25+25+252+252+....=100+2(50+25+252+.....)=100+2(S∞)=100+2(a1−r)=100+2(501−12)=100+2(5012)=100+2(100)=100+200=300
Jadi, total jarak yang ditempuh oleh kucing adalah 300 m. ♡
♠ Misal, Misal SA = jarak A yang ditempuh
dan Sk = jarak kucing yang ditempuh.
Rumus jarak : S=V.t dengan V jarak dan t adalah waktu.
Vk=2 m/s dan VA=1 m/s , artinya jarak yang ditempuh oleh A separuh dari jarak yang ditempuh oleh kucing. Berikut ilustrasi pergerakan kucing dan A .

♠ Menentukan total jarak yang ditempuh kucing
Dari ilustrasi gambar di atas, jarak total yang ditempuh kucing : Sk=100+50+50+25+25+252+252+....=100+2(50+25+252+.....)=100+2(S∞)=100+2(a1−r)=100+2(501−12)=100+2(5012)=100+2(100)=100+200=300
Jadi, total jarak yang ditempuh oleh kucing adalah 300 m. ♡
Nomor 5
Diketahui vektor →a=(−1,1,2),→u=(−1,c,2) dan →x=(−3,0,1). L1 adalah luas segitiga siku-siku yang dibentuk oleh →a
dan proyeksi vektor →a pada →x. L2 adalah luas segitiga siku-siku yang dibentuk oleh →u dan proyeksi vektor →u pada →x.
Jika L1=18L2, maka nilai 2c2=...
♣ Menentukan panjang dan perkalian dot
→a=(−1,1,2),→u=(−1,c,2) dan →x=(−3,0,1)
|→a|=√(−1)2+12+22=√6
|→u|=√(−1)2+c2+22=√c2+5
|→x|=√(−3)2+02+12=√10
→a.→x=(−1).(−3)+1.0+2.1=3+0+2=5
→u.→x=(−1).(−3)+c.0+2.1=3+0+2=5
♣ Konsep proyeksi skalar vektor (panjangnya)

Proyeksi skalar →a pada →x adalah →c dengan panjangnya : |→c|=→a.→x|→x|
♣ Proyeksi →a pada →x dan luasnya
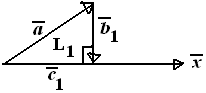
|→c1|=→a.→x|→x|=5√10=√102
Dengan pythagoras :
|→b1|=√|→a|2−|→c1|2=√(√6)2−(√102)2=12√14
L1=12.|→c1|.|→b1|=12.√102.12√14=√354
♣ Proyeksi →u pada →x dan luasnya
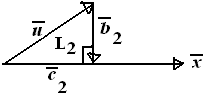
|→c2|=→u.→x|→x|=5√10=√102
Dengan pythagoras :
|→b2|=√|→u|2−|→c2|2=√(√c2+5)2−(√102)2=√2.√5+2c22
L2=12.|→c2|.|→b2|=12.√102.√2.√5+2c22=√5(5+2c2)4
♣ Menentukan nilai 2c2
L1=18L2√354=18.√5(5+2c2)4√35=√5(5+2c2)8(kuadratkan)35=5(5+2c2)64(bagi 5)7=(5+2c2)645+2c2=7.645+2c2=4482c2=443
Jadi, nilai 2c2=443.♡
→a=(−1,1,2),→u=(−1,c,2) dan →x=(−3,0,1)
|→a|=√(−1)2+12+22=√6
|→u|=√(−1)2+c2+22=√c2+5
|→x|=√(−3)2+02+12=√10
→a.→x=(−1).(−3)+1.0+2.1=3+0+2=5
→u.→x=(−1).(−3)+c.0+2.1=3+0+2=5
♣ Konsep proyeksi skalar vektor (panjangnya)

Proyeksi skalar →a pada →x adalah →c dengan panjangnya : |→c|=→a.→x|→x|
♣ Proyeksi →a pada →x dan luasnya

|→c1|=→a.→x|→x|=5√10=√102
Dengan pythagoras :
|→b1|=√|→a|2−|→c1|2=√(√6)2−(√102)2=12√14
L1=12.|→c1|.|→b1|=12.√102.12√14=√354
♣ Proyeksi →u pada →x dan luasnya

|→c2|=→u.→x|→x|=5√10=√102
Dengan pythagoras :
|→b2|=√|→u|2−|→c2|2=√(√c2+5)2−(√102)2=√2.√5+2c22
L2=12.|→c2|.|→b2|=12.√102.√2.√5+2c22=√5(5+2c2)4
♣ Menentukan nilai 2c2
L1=18L2√354=18.√5(5+2c2)4√35=√5(5+2c2)8(kuadratkan)35=5(5+2c2)64(bagi 5)7=(5+2c2)645+2c2=7.645+2c2=4482c2=443
Jadi, nilai 2c2=443.♡

Komentar ini telah dihapus oleh pengarang.
BalasHapusHallo Pak Putu. Pak saya mau tanya no 1. Itu kedua nilai k baik k=-4 maupun k=1/2 kok tidak membuat x2>2 ya Pak? apa tidak salah syarat pada soal nya Pak? Mohon pencerahannya Pak Putu, terimakasih banyak
BalasHapus