Pembahasan Soal UMPTN Matematika Dasar tahun 2001

Nomor 1

Nilai

$x \,$ yang menyebabkan pernyataan :
" Jika

$x^2 + x = 6 \,$ , maka

$\, x^2 + 3x < 9 \,$ "
Bernilai salah adalah ....

$\clubsuit \,$ Menentukan nilai

$\, x$

$x^2+x=6 \leftrightarrow x^2+x-6=0 \leftrightarrow (x-2)(x+3)=0 \leftrightarrow x=2 \vee x=-3$

$\clubsuit \,$ Cek kebenaran

$\begin{align} x=2 \rightarrow x^2+3x & < 9 \\ 2^2+3.2 & < 9 \\ 10 & < 9 \, \, \, \text{(salah)} \end{align}$

$\begin{align} x=-3 \rightarrow x^2+3x & < 9 \\ (-3)^2+3.(-3) & < 9 \\ 0 & < 9 \, \, \, \text{(benar)} \end{align}$

$\clubsuit \,$ Pernyataan " Jika P, maka Q" bernilai salah jika P benar dan Q salah.
Sehingga " Jika

$x^2 + x = 6 \,$ , maka

$\, x^2 + 3x < 9 \,$ " bernilai salah untuk

$\, x=2$
Jadi, pernyataan SALAH untuk

$\, x=2 . \heartsuit$

Nomor 2

Agar ketiga garis

$3x-y+1 = 0; \, 2x-y-3=0; \,$ dan

$\, x-ay-7 =0 \,$ berpotongan pada suatu titik, maka

$a \,$ harus bernilai ....

$\spadesuit \,$ Eliminasi pers(i) dan pers(ii)

$\begin{array}{cc} 3x-y+1 = 0 & \\ 2x-y-3=0 & - \\ \hline x = -4 & \end{array}$
pers(ii):

$2x-y-3=0 \rightarrow 2.(-4)-y-3=0 \rightarrow y = -11$
sehingga titik potongnya adalah (-4, -11)

$\spadesuit \,$ Substitusi titik potong ke pers(iii)

$x-ay-7 =0 \rightarrow (-4)-a.(-11)-7 =0 \rightarrow a = 1$
Jadi, nilai

$a = 1. \heartsuit$

Nomor 3

Misalkan

$f(x) = \left\{ \begin{array}{cc} 2x-1, & \text{untuk} \, \, \, \, 0 < x < 1 \\ x^2+1, & \text{untuk} \, \, x \, \, \text{yang lain} \end{array} \right.$
maka

$f(2)f(-4)+f\left( \frac{1}{2} \right) f(3) = ....$

$\clubsuit \,$ Fungsi

$f(x)$ berlaku sesuai nilai

$x$ yang disubstitusikan

$\clubsuit \,$ Menentukan nilai fungsi

$\begin{align} x = 2 \rightarrow f(x) & = x^2 + 1 \\ f(2) & = 2^2 + 1 = 5 \\ x = -4 \rightarrow f(x) & = x^2 + 1 \\ f(-4) & = (-4)^2 + 1 = 17 \\ x = \frac{1}{2} \rightarrow f(x) & = 2x - 1 \\ f(\frac{1}{2}) & = 2.(\frac{1}{2}) - 1 = 0 \\ x = 3 \rightarrow f(x) & = x^2 + 1 \\ f(3) & = (3)^2 + 1 = 10 \end{align}$

$\clubsuit \,$ Menentukan hasilnya

$f(2).f(-4)+f(\frac{1}{2}).f(3) = 5.17 + 0 . 10 = 85$
Jadi, hasilnya adalah 85.

$\heartsuit$

Nomor 4

Garis yang sejajar dengan garis

$2x+y=15 \,$ memotong kurva

$y = 6 + x - x^2 \,$ di titik (4, -6) dan ....

$\spadesuit \,$ Gambar

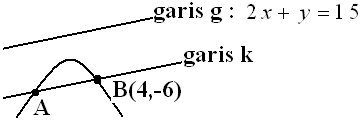
$\spadesuit \,$ Gradien garis g

$2x+y=15 \rightarrow m_g = \frac{-a}{b} = \frac{-2}{1} = -2$
Garis k sejajar dengan garis g, sehingga gradiennya sama :

$m_k = m_g = -2$

$\spadesuit \,$ Persamaan garis k

$y-y_1 = m(x-x_1) \rightarrow y-(-6) = -2(x-4) \rightarrow y = -2x + 2$

$\spadesuit \,$ Menentukan titik potong garis k dan parabola

$\begin{align} y_1 & = y_2 \\ -2x+2 & = 6+x-x^2 \\ x^2-3x-4 & = 0 \\ (x+1)(x-4) & = 0 \\ x=-1 & \vee x = 4 \\ x= -1 \rightarrow & y = -2x+2 = -2(-1)+2 = 4 \\ x= 4 \rightarrow & y = -2x+2 = -2(4)+2 = -6 \end{align}$
sehingga titik potongnya : (4,-6) dan (-1,4)
Jadi, titik potong yang lain adalah (-1,4).

$\heartsuit$

Nomor 5

Persamaan kuadrat

$\, 3x^2-(a-1)x-1=0 \,$ mempunyai akar - akar

$x_1 \,$ dan

$\, x_2 \,$ , sedangkan persamaan kuadrat yang akar-akarnya

$\frac{1}{x_1} \,$ dan

$\frac{1}{x_2} \,$ adalah

$\, x^2-(2b+1)x+b=0 \,$ . Nilai

$\, 2a + b = ....$

$\clubsuit \,$ PK I :

$3x^2 - (a-1)x - 1 = 0 \,$ akar-akarnya

$x_1 \,$ dan

$\, x_2$

$x_1+x_2 = \frac{-b}{a} = \frac{a-1}{3} \,$ dan

$\, x_1.x_2 = \frac{c}{a} = -\frac{1}{3}$
PK II :

$x^2-(2a+1)x+b = 0 \,$ akar-akarnya

$y_1 = \frac{1}{x_1} \,$ dan

$\, y_2 = \frac{1}{x_2} \,$ Operasi akar-akar PK II

$\begin{align} \text{operasi} & \text{ perkalian} : \, \, \\ y_1.y_2 & = \frac{c}{a} \\ \frac{1}{x_1} . \frac{1}{x_2} & = \frac{b}{1} \\ \frac{1}{x_1.x_2} & = b \\ \frac{1}{-\frac{1}{3}} & = b \\ -3 & = b \end{align}$

$\begin{align} \text{operasi} & \text{ penjumlahan} : \\ y_1+y_2 & = \frac{-b}{a} \\ \frac{1}{x_1} + \frac{1}{x_2} & = \frac{b}{1} \\ \frac{x_1+x_2}{x_1.x_2} & = \frac{2b+1}{1} \\ \frac{\frac{a-1}{3}}{-\frac{1}{3}} & = 2b+1 \\ 1-a & = 2b + 1 \\ 1-a & = 2.(-3) + 1 \rightarrow a = 6 \end{align}$

sehingga :

$2a + b = 2.6 + (-3) = 9$
Jadi, nilai

$2a + b = 9. \heartsuit$

Nomor Soal Lainnya : 1-5 6-10 11-15 16-20 21-25 26-30