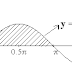
Pembahasan Soal SPMB Matematika IPA tahun 2002

Nomor 1

Daerah

$D$ dibatasi oleh grafik fungsi

$y = \frac{1}{\sqrt{x}} , \,$ garis

$x = 1, \,$ garis

$x = 4, \,$ dan sumbu X. Jika garis

$x = c \,$ memotong daerah

$D$ sehingga menjadi daerah

$D_1$ dan

$D_2$ yang luasnya sama, maka

$c = ....$

$\clubsuit \,$ gambar

$\clubsuit \,$ Menentukan nilai

$c$

$\begin{align} L_{D1} & = L_{D2} \\ \int \limits_1^c \frac{1}{\sqrt{x}} \, dx & = \int \limits_c^4 \frac{1}{\sqrt{x}} \, dx \\ \int \limits_1^c x^{-\frac{1}{2}} \, dx & = \int \limits_c^4 x^{-\frac{1}{2}} \, dx \\ [2x^{\frac{1}{2}}]_1^c & = [2x^{\frac{1}{2}}]_c^4 \, \, \text{(bagi 2)} \\ [\sqrt{x}]_1^c & = [\sqrt{x}]_c^4 \\ \sqrt{c} - \sqrt{1} & = \sqrt{4} - \sqrt{c} \\ \sqrt{c} - 1 & = 2 - \sqrt{c} \\ 2\sqrt{c} & = 3 \\ \sqrt{c} & = \frac{3}{2} \\ c & = \frac{9}{4} \end{align}$
Jadi, nilai

$c = \frac{9}{4} . \heartsuit$

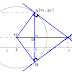
Nomor 2

Bidang V dan W berpotongan tegak lurus sepanjang garis

$g$ . Garis

$l$ membentuk sudut

$45^\circ$ dengan V dan

$30^\circ$ dengan W. Sinus sudut antara

$l$ dan

$g$ adalah .....

$\spadesuit \,$ Gambar

BC = garis

$g$
sudut antara garis

$l$ dan

$g$ =

$\angle$ ABC =

$\theta , \,$ sehingga harus ditentukan ukuran sisi-sisi

$\Delta ABC$

$\spadesuit \,$ Menentukan ukuran segitiganya
*).

$\Delta ABD, \,$ sudut ADB 45

$^\circ$ sehingga sudut ABD juga 45

$^\circ$ , yang artinya segitiga ABD siku-siku sama kaki. Misal panjang BD = DA = 2, maka panjang AB = 2

$\sqrt{2} \,$ (dengan pythagoras).
*).

$\Delta BEA, \,$ dengan BA =

$2\sqrt{2} \,$ dan sudut ABE =

$30^\circ . \,$ Untuk menentukan panjang BE dan EA dapat menggunakan aturan sin dan cos pada sudut ABE.
*). Sisi-sisi segitiga BCE dan CEA dapat dilengkapi dengan teorema pythagoras.
*). Diperolehlah panjang sisi-sisi segitiga ABC seperti gambar di atas.

$\spadesuit \,$ Menentukan nilai

$\cos \theta \,$ dengan aturan cosinus pada

$\Delta ABC$

$\begin{align} AC^2 & = BC^2 + BA^2 - 2.BC.BA. \cos ABC \\ \cos ABC & = \frac{BC^2 + BA^2 - AC^2}{2.BC.BA} \\ \cos \theta & = \frac{(\sqrt{2})^2 + (2\sqrt{2})^2 - (\sqrt{6})^2}{2.\sqrt{2}.2\sqrt{2}} \\ \cos \theta & = \frac{2 + 8 - 6}{8} = \frac{4}{8} = \frac{1}{2} \end{align}$

Seingga nilai :

$\sin \theta = \frac{1}{2} \sqrt{3}$
Jadi, nilai

$\sin \theta = \frac{1}{2} \sqrt{3} . \heartsuit$

Nomor 3

$u_1, u_2, u_3, .......... \,$ adalah barisan aritmetika dengan suku - suku positif, jika

$u_1+u_2+u_3 = 24 \,$ dan

$u_1^2 = u_3 -10 \,$ maka

$u_4 = .....$

$\clubsuit \,$ Barisan aritmetika :

$u_n = a + (n-1)b$

$\clubsuit \,$ Menentukan hubungan

$a$ dan

$b$

$\begin{align} u_1+u_2+u_3 & = 24 \\ a+(a+b)+(a+2b) & = 24 \\ 3a+3b & = 24 \, \, \text{(bagi 3)} \\ a+b & = 8 \\ b & = 8 - a \, \, \text{....pers(i)} \end{align}$

$\clubsuit \,$ Menentukan nilai

$a$

$\begin{align} u_1^2 & = u_3 -10 \\ a^2 & = (a+2b) -10 \, \, \text{( substitusi pers(i) )} \\ a^2 & = a+2(8-a) -10 \\ a^2 + a - 6 & = 0 \\ (a-2)(a+3) & = 0 \\ a = 2 \vee a & = -3 \end{align}$
Karena suku-suku positif, maka

$a = 2 \,$ yang memenuhi.
pers(i):

$b = 8 - a = 8 - 2 = 6$
sehingga

$u_4 = a + 3b = 2 + 3.6 = 2 + 18 = 20$
Jadi, nilai

$u_4 = 20 . \heartsuit$

Nomor 4

Jika

$\sin \left( A - \frac{\pi}{4} \right) - 5\cos \left( A - \frac{\pi}{4} \right) = 0,$ maka

$\tan A = .....$

$\spadesuit \,$ Konsep dasar

$\tan x = \frac{\sin x}{\cos x }$

$\tan (A - B) = \frac{\tan A - \tan B}{1+\tan A.\tan B}$

$\spadesuit \,$ Menyederhanakan soal

$\begin{align} \sin \left( A - \frac{\pi}{4} \right) - 5\cos \left( A - \frac{\pi}{4} \right) & = 0 \\ \sin \left( A - \frac{\pi}{4} \right) & = 5\cos \left( A - \frac{\pi}{4} \right) \\ \frac{\sin \left( A - \frac{\pi}{4} \right)}{\cos \left( A - \frac{\pi}{4} \right)} & = 5 \\ \tan \left( A - \frac{\pi}{4} \right) & = 5 \\ \frac{\tan A - \tan \frac{\pi}{4}}{1+\tan A.\tan \frac{\pi}{4}} & = 5 \\ \frac{\tan A - 1}{1+\tan A.1} & = 5 \\ \frac{\tan A - 1}{1+\tan A} & = 5 \\ \tan A - 1 & = 5 + 5\tan A \\ 4\tan A & = -6 \\ \tan A & = \frac{-6}{4} = \frac{-3}{2} \end{align}$
Jadi, nilai

$\tan A = \frac{-6}{4} = \frac{-3}{2} . \heartsuit$

Nomor 5

Himpunan penyelesaian

$2^{2-2x} + 2 > \frac{9}{2^x}, \, x \in R \,$ adalah .....

$\clubsuit \,$ konsep eksponen :

$a^{m-n} = \frac{a^m}{a^n}$

$\clubsuit \,$ Misal

$p = 2^x$ ,

$\begin{align} 2^{2-2x} + 2 & > \frac{9}{2^x} \\ \frac{2^2}{2^{2x}} + 2 & > \frac{9}{2^x} \\ \frac{4}{(2^{x})^2} + 2 & > \frac{9}{2^x} \\ \frac{4}{p^2} + 2 & > \frac{9}{p} \, \, \text{( kali } \, p^2 ) \\ 4 + 2p^2 & > 9p \\ 2p^2 - 9p + 4 & > 0 \\ (2p-1)(p-4) & > 0 \\ p = \frac{1}{2} \rightarrow 2^x & = \frac{1}{2} \rightarrow x = -1 \\ p = 4 \rightarrow 2^x & = 4 \rightarrow x = 2 \end{align}$