Pembahasan Soal SBMPTN Matematika IPA kode 532 tahun 2014

Nomor 1

Jika

$A(x) = \frac{1}{2}\left( p^x - p^{-x} \right) \,$ dan

$B(x) = \frac{1}{2}\left( p^x + p^{-x} \right) \,$ denga

$p > 1 \,$ , maka

$B(nx) = ....$
(A)

$\left( B(x) - A(x) \right)^\frac{1}{n} + A\left( \frac{x}{n} \right)$
(B)

$\left( B(x) - A(x) \right)^\frac{1}{n} + A\left( nx \right)$
(C)

$\left( B(x) - A(x) \right)^n + A\left( nx \right)$
(D)

$\left( A(x) - B(x) \right)^n + A\left( nx \right)$
(E)

$\left( A(x) - B(x) \right)^n + A\left( \frac{x}{n} \right)$

$\clubsuit \,$ Menentukan

$B(nx) \,$

$\begin{align} B(x) & = \frac{1}{2}\left( p^x + p^{-x} \right) \\ B(nx) & = \frac{1}{2}\left( p^{nx} + p^{-nx} \right) \, \, \, \text{ ...pers(i)} \end{align}$
Karena pada pilihannya dalam bentuk

$A(nx) \,$ atau

$A(\frac{x}{n}) \,$ , maka pers(i) harus diubah atau dimodifikasi menjadi bentuk

$A(nx) \,$ atau

$A(\frac{x}{n}) \,$ .

$\clubsuit \,$ Memodifikasi pers(i)

$\begin{align} B(nx) & = \frac{1}{2}\left( p^{nx} + p^{-nx} \right) \\ B(nx) & = \frac{1}{2}\left( p^{nx} \right) + \frac{1}{2}\left( p^{-nx} \right) \\ B(nx) & = \frac{1}{2}\left( p^{nx} \right) + p^{-nx} - \frac{1}{2}\left( p^{-nx} \right) \\ B(nx) & = p^{-nx} + \frac{1}{2}\left( p^{nx} - p^{-nx} \right) \\ B(nx) & = p^{-nx} + A(nx) \, \, \, \text{ ...pers(ii)} \end{align}$

$\clubsuit \,$ Memodifikasi bentuk

$p^{-nx}$

$\begin{align} p^{-nx} & = (p^{-x})^n \\ & = ( \frac{1}{2} . p^{-x} + \frac{1}{2} . p^{-x} )^n \\ & = ( \frac{1}{2} . p^{-x} + \frac{1}{2} . p^{-x} + \frac{1}{2} . p^{x} - \frac{1}{2} . p^{x} )^n \\ & = ( \frac{1}{2} . p^{x} + \frac{1}{2} . p^{-x} - \frac{1}{2} . p^{x} + \frac{1}{2} . p^{-x} )^n \\ & = \left( \frac{1}{2} (p^{x} + p^{-x}) - \frac{1}{2} (p^{x} - p^{-x} ) \right)^n \\ p^{-nx} & = \left( B(x) - A(x) \right)^n \, \, \, \text{ ...pers(iii)} \end{align}$

$\clubsuit \,$ Substitusi pers(iii) ke pers(ii)

$\begin{align} B(nx) & = p^{-nx} + A(nx) \\ B(nx) & = \left( B(x) - A(x) \right)^n + A(nx) \end{align}$
Jadi, diperoleh bentuk

$B(nx) = \left( B(x) - A(x) \right)^n + A(nx) . \heartsuit$

Nomor 2

Diberikan kubus ABCD.EFGH dengan panjang rusuk

$3p . \,$ Titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD sehingga BP = GQ = DR =

$p \,$ . Jika S adalah titik potong bidang yang melalui P, Q, dan R dengan rusuk DH, maka jarak dari S ke P adalah .....

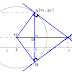
$\spadesuit \,$ Gambar bidang irisannya

Perpotongan bidang yang melalui titik P, Q, dan R dengan rusuk DH adalah Bidang irisan (bidang VPQZSR) dengan rusuk DH yaitu di titik S.
Ternyata jarak DS sama dengan BP , sehingga jarak SP sama saja dengan jarak BD yaitu panjang diagonal sisi.
Misal panjang rusuknya adalah

$s \,$ dengan

$s = 3p$

$\spadesuit \,$ Menentukan jarak S ke P

$\begin{align} \text{jarak S ke P } & = \text{ Panjang BD (Diagonal sisi) } \\ & = s\sqrt{2} \\ & = 3p\sqrt{2} \end{align}$
Jadi, jarak S ke P adalah

$3p\sqrt{2} . \heartsuit$

Nomor 3

Banyaknya akar real

$f(t)=t^9-t$ adalah ... buah.

$\spadesuit \,$ Bentuk pemfaktoran :

$p^2-q^2=(p-q)(p+q)\,$ atau

$\, p^n-1=(p^{n/2}-1)(p^{n/2}+1)$
dengan

$n$ genap

$\spadesuit \,$ Untuk menentukan akar-akarnya, maka

$f(t)=0$

$\begin{align} f(t)&=0 \\ t^9-t&=0 \\ t(t^8-1)&=0 \\ t(t^4-1)(t^4+1)&=0 \\ t(t^2-1)(t^2+1)(t^4+1)&=0 \\ t(t-1)(t+1)(t^2+1)(t^4+1)&=0 \end{align}$

$\spadesuit \,$ Sehingga akar-akarnya:

$t=0,t=1,t=-1$ dan

$t^2=-1$ (tidak real) serta

$t^4=-1$ (tidak real).
Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1.

$\, \heartsuit$

Nomor 4

Tujuh anak laki-laki dan tiga perempuan akan duduk berdampingan dalam satu baris. Peluang kedua ujung ditempati anak laki-laki dan tidak ada anak perempuan duduk berdampingan adalah .....

$\spadesuit \,$ Ada 7L dan 3P duduk berdampingan, sehingga

$n(S) = 10!$
Pada kasus orang duduk, urutan atau letak diperhatikan sehingga menggunakan permutasi. Rumus :

$P_r^n = \frac{n!}{(n-r)!}$

$\spadesuit \,$ Susunan agar kedua ujung ditempati anak laki-laki dan tidak ada anak perempuan duduk berdampingan, ada dua kemungkinan :

Keterangan Kasus I :
*). dua anak laki-laki dipilih dari 7 anak laki-laki untuk menempati kedua ujung , ada

$P_2^7 = \frac{7!}{(7-2)!} = \frac{7!}{5!} = 7.6 \,$ cara
*). agar tidak ada anak perempuan berdampingan, maka 8 posisi yang ditengah harus dikelompokkan seperti gambar kasus I menjadi lima kelompok dengan tiga kelompok berpasangan (ada anak laki dan perempuan dengan perempuan didepan dan laki-laki dibelakangnya).
*). lima kelompok yang ada bisa diacak urutannya , ada

$5! \,$ cara.
*). karena lima kelompok sudah diacak, maka tinggal menentukan tiga anak laki-laki dari 5 anak laki-laki untuk berpasangan dengan tiga anak perempuan, ada

$P_3^5 = \frac{5!}{(5-3)!}=\frac{5!}{2!} = 5.4.3$
total cara I =

$P_2^7 . 5!. P_3^5$
Keterangan kasus II :
*). kasus II mirip dengan kasus I, hanya saja untuk kelompok yang berpasangan urutannya dibalik yaitu laki-laki dulu baru perempuan.
total cara II =

$P_2^7 . 5!. P_3^5$

$\spadesuit \,$ Sehingga total cara :

$n(A) = \,$ total cara I + total cara II

$n(A) = \,$ =

$2. ( P_2^7 . 5!. P_3^5 ) \,$ = 2.7.6.5!.5.4.3

$\spadesuit \,$ Menentukan peluang

$P(A)$

$\begin{align} P(A) & = \frac{n(A)}{n(S)} \\ & = \frac{2.7.6.5!.5.4.3}{10!} \\ & = \frac{2.7.6.5!.5.4.3}{10.9.8.7.6.5!} \\ & = \frac{1}{6} \\ \end{align}$
Jadi, peluangnya adalah

$\frac{1}{6} . \heartsuit$

Nomor 5

Nilai maksimum

$f(x) = 2x + \sqrt{p-4x} \,$ adalah

$\frac{13}{2} . \,$ Nilai

$f(2) + f^\prime (2) \,$ adalah ....

$\clubsuit \,$ Konsep turunan bentuk akar

$y = \sqrt{g(x)} \rightarrow y^\prime = \frac{g^\prime (x)}{2\sqrt{g(x)}}$

$\clubsuit \,$ Menentukan turunan fungsi

$f(x)$

$\begin{align} f(x) & = 2x + \sqrt{p-4x} \\ f^\prime (x) & = 2 + \frac{-4}{2\sqrt{p-4x}} \\ f^\prime (x) & = 2 - \frac{2}{\sqrt{p-4x}} \end{align}$

$\clubsuit \,$ Fungsi

$f(x) \,$ maksimum, syaratnya :

$f^\prime (x) = 0$

$\begin{align} f^\prime (x) & = 0 \\ 2 - \frac{2}{\sqrt{p-4x}} & = 0 \\ \frac{2}{\sqrt{p-4x}} & = 2 \\ 2\sqrt{p-4x} & = 2 \, \, \, \text{(bagi 2)} \\ \sqrt{p-4x} & = 1 \, \, \, \text{(kuadratkan)} \\ \left( \sqrt{p-4x} \right)^2 & = 1^2 \\ p-4x & = 1 \\ x & = \frac{p-1}{4} \end{align}$
artinya fungsi

$f(x) \,$ maksimum pada saat

$x = \frac{p-1}{4} \,$

$\clubsuit \,$ Substitusi

$x = \frac{p-1}{4} \,$ ke fungsi

$f(x) \,$ diperoleh nilai maksimum

$\begin{align} x = \frac{p-1}{4} \rightarrow f(x) & = 2x + \sqrt{p-4x} \\ f_\text{maks} \left( \frac{p-1}{4} \right) & = \frac{13}{2} \\ 2.\left( \frac{p-1}{4} \right) + \sqrt{p-4.\left( \frac{p-1}{4} \right)} & = \frac{13}{2} \\ \frac{p-1}{2} + 1 & = \frac{13}{2} \, \, \, \text{(kali 2)} \\ p-1 + 2 & = 13 \\ p & = 12 \end{align}$
Sehingga fungsinya :

$f(x) = 2x + \sqrt{12-4x}$
dan turunannya :

$f^\prime (x) = 2 - \frac{2}{\sqrt{12-4x}}$

$\clubsuit \,$ Menentukan hasilnya

$\begin{align} f(2) + f^\prime (2) & = \left( 2.2 + \sqrt{12-4.2} \right) + \left( 2 - \frac{2}{\sqrt{12-4.2}} \right) \\ & = \left( 4 + \sqrt{12-8} \right) + \left( 2 - \frac{2}{\sqrt{12-8}} \right) \\ & = \left( 4 + \sqrt{4} \right) + \left( 2 - \frac{2}{\sqrt{4}} \right) \\ & = \left( 4 + 2 \right) + \left( 2 - \frac{2}{2} \right) \\ & = 6 + \left( 2 - 1 \right) \\ f(2) + f^\prime (2) & = 7 \end{align}$
Jadi, nilai

$f(2) + f^\prime (2) = 7 . \heartsuit$

Nomor Soal Lainnya : 1-5 6-10 11-15