Nomor 1
Banyaknya akar real f(t)=t9−t adalah ... buah.
♣ Bentuk pemfaktoran :
p2−q2=(p−q)(p+q) atau pn−1=(pn/2−1)(pn/2+1)
dengan n genap
♣ Untuk menentukan akar-akarnya, maka f(t)=0
f(t)=0t9−t=0t(t8−1)=0t(t4−1)(t4+1)=0t(t2−1)(t2+1)(t4+1)=0t(t−1)(t+1)(t2+1)(t4+1)=0
♣ Sehingga akar-akarnya:
t=0,t=1,t=−1 dan t2=−1 (tidak real) serta t4=−1 (tidak real).
♣ Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. ♡
p2−q2=(p−q)(p+q) atau pn−1=(pn/2−1)(pn/2+1)
dengan n genap
♣ Untuk menentukan akar-akarnya, maka f(t)=0
f(t)=0t9−t=0t(t8−1)=0t(t4−1)(t4+1)=0t(t2−1)(t2+1)(t4+1)=0t(t−1)(t+1)(t2+1)(t4+1)=0
♣ Sehingga akar-akarnya:
t=0,t=1,t=−1 dan t2=−1 (tidak real) serta t4=−1 (tidak real).
♣ Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. ♡
Nomor 2
Jika C(t)=1tt∫0(f(s)+g(s))ds dan lima→0C(t0+a)−C(t0)a=0,
maka C(t0)=...
♠ Misal hasil integral f(s) adalah F(s) dan g(s) adalah G(s).
C(t)=1tt∫0(f(s)+g(s))dsC(t)=1t[F(s)+G(s)]t0C(t)=1t[F(t)+G(t)−F(0)−G(0)]t.C(t)=[F(t)+G(t)−F(0)−G(0)]...pers(i)
♠F(0) dan G(0) adalah konstanta, sehingga turunannya sama dengan nol, dan turunan F(t),G(t) berturut-turut adalah f(t) dan g(t)
♠ Turunan pers(i) terhadap t:
1.C(t)+t.C′(t)=f(t)+g(t) ...pers(ii)
♠ Menyelesaikan limit dengan cara diturunkan terhadap a:
lima→0C(t0+a)−C(t0)a=0lima→0C′(t0+a)1=0C′(t0+0)=0C′(t0)=0....pers(iii)
♠ Gunakan pers(iii) dan substitusikan t=t0 ke pers (ii) :
1.C(t)+t.C′(t)=f(t)+g(t)C(t0)+t0.C′(t0)=f(t0)+g(t0)C(t0)+t0.0=f(t0)+g(t0)C(t0)=f(t0)+g(t0)
Jadi, C(t0)=f(t0)+g(t0).♡
C(t)=1tt∫0(f(s)+g(s))dsC(t)=1t[F(s)+G(s)]t0C(t)=1t[F(t)+G(t)−F(0)−G(0)]t.C(t)=[F(t)+G(t)−F(0)−G(0)]...pers(i)
♠F(0) dan G(0) adalah konstanta, sehingga turunannya sama dengan nol, dan turunan F(t),G(t) berturut-turut adalah f(t) dan g(t)
♠ Turunan pers(i) terhadap t:
1.C(t)+t.C′(t)=f(t)+g(t) ...pers(ii)
♠ Menyelesaikan limit dengan cara diturunkan terhadap a:
lima→0C(t0+a)−C(t0)a=0lima→0C′(t0+a)1=0C′(t0+0)=0C′(t0)=0....pers(iii)
♠ Gunakan pers(iii) dan substitusikan t=t0 ke pers (ii) :
1.C(t)+t.C′(t)=f(t)+g(t)C(t0)+t0.C′(t0)=f(t0)+g(t0)C(t0)+t0.0=f(t0)+g(t0)C(t0)=f(t0)+g(t0)
Jadi, C(t0)=f(t0)+g(t0).♡
Nomor 3
Banyak cara menyusun 4 buku matematika, 3 buku fisika, dan 2 buku kimia sehingga buku-buku sejenis dalam satu kelompok adalah...
♣ Ada 3 jenis buku (mat, fis, kim) yang akan disusun dengan susunan sebanyak 3! cara = 6 cara
♣ Masing-masing buku berkelompok dengan penyusunan :
4 mat ⇒ 4! cara = 24 cara
3 fis ⇒ 3! cara = 6 cara
2 kim ⇒ 2! cara = 2 cara
♣ Jadi total penyusunan buku-buku tersebut :
3! . (4! . 3!. 2!) = 6 . 24. 6. 2 = 1728 cara. ♡
♣ Masing-masing buku berkelompok dengan penyusunan :
4 mat ⇒ 4! cara = 24 cara
3 fis ⇒ 3! cara = 6 cara
2 kim ⇒ 2! cara = 2 cara
♣ Jadi total penyusunan buku-buku tersebut :
3! . (4! . 3!. 2!) = 6 . 24. 6. 2 = 1728 cara. ♡
Nomor 4
Jika 3sinx+4cosy=5, maka nilai maksimum 3cosx+4siny adalah ...
♠ Kuadratkan persamaan 3sinx+4cosy=5:
(3sinx+4cosy)2=529sin2x+16cos2y+24sinxcosy=25(sin2z+cos2z=1)9(1−cos2x)+16(1−sin2y)+24sinxcosy=259−9cos2x+16−16sin2y+24sinxcosy=259cos2x+16sin2y=24sinxcosy...pers(i)
♠ Misalkan f=3cosx+4siny, dikuadratkan:
f2=(3cosx+4siny)2f2=9cos2x+16sin2y+24cosxsiny...pers(ii)
♠ Substitusi pers (i) ke pers(ii) :
f2=9cos2x+16sin2y+24cosxsiny=24sinxcosy+24cosxsiny=24(sinxcosy+cosxsiny)f2=24sin(x+y)
♠ Nilai maksimum dari , y=Asinf(x)⇒ymax=|A| :
f2=24sin(x+y)f2max=|24|f2max=24fmax=√24fmax=2√6
Jadi, nilai maksimum dari 3cosx+4siny=2√6.♡
(3sinx+4cosy)2=529sin2x+16cos2y+24sinxcosy=25(sin2z+cos2z=1)9(1−cos2x)+16(1−sin2y)+24sinxcosy=259−9cos2x+16−16sin2y+24sinxcosy=259cos2x+16sin2y=24sinxcosy...pers(i)
♠ Misalkan f=3cosx+4siny, dikuadratkan:
f2=(3cosx+4siny)2f2=9cos2x+16sin2y+24cosxsiny...pers(ii)
♠ Substitusi pers (i) ke pers(ii) :
f2=9cos2x+16sin2y+24cosxsiny=24sinxcosy+24cosxsiny=24(sinxcosy+cosxsiny)f2=24sin(x+y)
♠ Nilai maksimum dari , y=Asinf(x)⇒ymax=|A| :
f2=24sin(x+y)f2max=|24|f2max=24fmax=√24fmax=2√6
Jadi, nilai maksimum dari 3cosx+4siny=2√6.♡
Nomor 5
Diberikan kubus ABCD.EFGH dengan panjang rusuk 3p. Titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD sehingga BP=GQ=DR=p.
Misalkan β adalah irisan bidang yang melalui P, Q, dan R. Luas alas yang berada di bawah bidang β adalah ... p2.
♣ Gambar bidang irisan (bidang β):


♣ Bidang alas di bawah bidang β
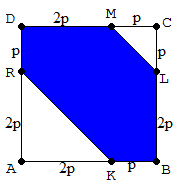
Lalas=LABCD−(LAKR+LLCM)=(3p)2−(12.2p.2p+12.p.p)Lalas=9p2−52p2=132p2
♣ Sehingga:
LalasLABCD=132p29p2=1318
Jadi, Lalas=1318LABCD.♡


♣ Bidang alas di bawah bidang β

Lalas=LABCD−(LAKR+LLCM)=(3p)2−(12.2p.2p+12.p.p)Lalas=9p2−52p2=132p2
♣ Sehingga:
LalasLABCD=132p29p2=1318
Jadi, Lalas=1318LABCD.♡










Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.