Hallow sobat, bagaimana kabarnya???? Mudah-mudahan baik-baik saja!!!!
Berikut kami share pembahasan soal SBMPTN Matematika IPA kode 542 tahun 2014 untuk kode yang ke enam matematika IPA tahun 2014. Lumayan bisa untuk latihan bagi adik-adik untuk enam kode yang ada, dan jika sobat ada yang mempunyai soal SBMPTN dengan kode yang berbeda, mohon share ke blog kami ya, atau krim ke email kami d.4rm.408@gmail.com langsung. Terima kasih sebelumnya.
Soal SBMPTN Matematika IPA kode 542 ini sama dengan kode 591 , yang artinya soalnya akan sama dengan kode yang lainnya yaitu kode 541,543,544, 592,593, dan kode 594, hanya saja nomor soalnya yang diacak. Selamat belajar teman-teman, semoga bermanfaat.
Untuk soal nomor satu melibatkan materi persamaan kuadrat dan turunan yang digunakan untuk menentukan nilai minimumnya. di sini kita menyediakan dua alternatif penyelesaian. Untuk soal nomor dua melibatkan teori trigonometri dan deret geometri tak hingga serta bentuk pertidaksamaan. Dari pilihan jawaban, sebenarnya yang diminta adalah rentang nilai s dengan menerapkan deret tak hingga dan nilai maksimum/minimum fungsi trigonometri.
Pada soal nomor 3 relatif mudah karena hanya butuh kemampuan untuk memfaktorkan suatu bentuk persamaan suku banyak (polinomial) dan mampu memilih jenis akar-akar realnya (bilangan real) . Penerapan kaidah pencacahan yaitu permutasi berulang digunakan untuk menyelesaikan soal nomor 4. mohon maaf karena disini kita menyelesaikannya harus dengan mendaftar seperti itu, jika ada alternatif lain mohon untuk di share di sini ya.
Soal nomor 5 melibatkan konsep dimensi tiga yang menitik beratkan pada bidang irisan. Pada soal ini, yang sulit memang menentukan dan menggambar bidang irisannya. Salah satu cara yang bisa kita gunakan adalah dengan bantuan sumbu afinitas (garis afinitas = garis yang terbentuk dari perpotongan bidang irisan dengan bidang alas)
Nomor 1
Jika p dan q merupakan akar-akar persamaan kuadrat : x2−(a+1)x+(−a−52)=0
maka nilai minimum p2+q2 adalah ....
♣ PK : x2−(a+1)x+(−a−52)=0 akar-akarnya p dan q
Operasi akar-akarnya :
p+q=−ba=a+11=a+1 dan p.q=ca=−a−52
♣ Menentukan bentuk p2+q2
p2+q2=(p+q)2−2pqf(a)=(a+1)2−2(−a−52)f(a)=a2+2a+1+2a+5f(a)=a2+4a+6
♣ Menentukan nilai minimum, syarat : f′(a)=0
f(a)=a2+4a+6f′(a)=2a+4f′(a)=02a+4=0→a=−2
artinya p2+q2 minimum saat a=−2
♣ Substitusi nilai a=−2
a=−2→p2+q2=f(a)=a2+4a+6f(−2)=(−2)2+4(−2)+6=4−8+6=2
Jadi, nilai minimum p2+q2 adalah 2 . ♡
Operasi akar-akarnya :
p+q=−ba=a+11=a+1 dan p.q=ca=−a−52
♣ Menentukan bentuk p2+q2
p2+q2=(p+q)2−2pqf(a)=(a+1)2−2(−a−52)f(a)=a2+2a+1+2a+5f(a)=a2+4a+6
♣ Menentukan nilai minimum, syarat : f′(a)=0
f(a)=a2+4a+6f′(a)=2a+4f′(a)=02a+4=0→a=−2
artinya p2+q2 minimum saat a=−2
♣ Substitusi nilai a=−2
a=−2→p2+q2=f(a)=a2+4a+6f(−2)=(−2)2+4(−2)+6=4−8+6=2
Jadi, nilai minimum p2+q2 adalah 2 . ♡
Cara II : Menggunakan diskriminan
♣ PK : x2−(a+1)x+(−a−52)=0 akar-akarnya p dan q
Operasi akar-akarnya :
p+q=−ba=a+11=a+1 dan p.q=ca=−a−52
♣ Menentukan bentuk p2+q2
p2+q2=(p+q)2−2pqf(a)=(a+1)2−2(−a−52)f(a)=a2+2a+1+2a+5f(a)=a2+4a+6
♣ Karena fungsinya berbentuk fungsi kuadrat, sehingga nilai minimumnya adalah D−4a
f(a)=a2+4a+6→a=1,b=4,c=6fminimum=D−4a=b2−4ac−4a=42−4.1.6−4.1fminimum=−8−4=2
Jadi, nilai minimum p2+q2 adalah 2 . ♡
♣ PK : x2−(a+1)x+(−a−52)=0 akar-akarnya p dan q
Operasi akar-akarnya :
p+q=−ba=a+11=a+1 dan p.q=ca=−a−52
♣ Menentukan bentuk p2+q2
p2+q2=(p+q)2−2pqf(a)=(a+1)2−2(−a−52)f(a)=a2+2a+1+2a+5f(a)=a2+4a+6
♣ Karena fungsinya berbentuk fungsi kuadrat, sehingga nilai minimumnya adalah D−4a
f(a)=a2+4a+6→a=1,b=4,c=6fminimum=D−4a=b2−4ac−4a=42−4.1.6−4.1fminimum=−8−4=2
Jadi, nilai minimum p2+q2 adalah 2 . ♡
Nomor 2
Jika s=1+12sin2x+14sin22x+18sin32x+.... , maka .... .
(A) 23<s<2
(B) 32<s<2
(C) 23<s<32
(D) 12<s<32
(E) 12<s<23
(A) 23<s<2
(B) 32<s<2
(C) 23<s<32
(D) 12<s<32
(E) 12<s<23
♠ Konsep Deret tak hingga : s∞=a1−r
s=1+12sin2x+14sin22x+18sin32x+....
a=1, dan r=u2u1=12sin2x1=12sin2x
♠ Menentukan jumlahnya
s=1+12sin2x+14sin22x+18sin32x+....s=s∞=a1−rs=11−12sin2x
nilai maksimum dan minimum dari sin2x 1 dan -1.
*) Nilai maksimum dari s=11−12sin2x diperoleh pada saat nilai penyebutnya minimum, bentuk 1−12sin2x minimum saat nilai sin2x maksimum, sehingga nilai sin2x=1
**) Nilai minimum dari s=11−12sin2x diperoleh pada saat nilai penyebutnya maksimum, bentuk 1−12sin2x maksimum saat nilai sin2x minimum, sehingga nilai sin2x=−1
♠ Menentukan rentang nilai s
sin2x=1→s=11−12sin2xsmaks=11−12.1smaks=11−12=112=2sin2x=−1→s=11−12sin2xsmin=11−12.(−1)smin=11+12=132=23
Sehingga rentang nilai s adalah min<s<maks yaitu 23<s<2
Jadi, nilai s ada pada interval 23<s<2.♡
s=1+12sin2x+14sin22x+18sin32x+....
a=1, dan r=u2u1=12sin2x1=12sin2x
♠ Menentukan jumlahnya
s=1+12sin2x+14sin22x+18sin32x+....s=s∞=a1−rs=11−12sin2x
nilai maksimum dan minimum dari sin2x 1 dan -1.
*) Nilai maksimum dari s=11−12sin2x diperoleh pada saat nilai penyebutnya minimum, bentuk 1−12sin2x minimum saat nilai sin2x maksimum, sehingga nilai sin2x=1
**) Nilai minimum dari s=11−12sin2x diperoleh pada saat nilai penyebutnya maksimum, bentuk 1−12sin2x maksimum saat nilai sin2x minimum, sehingga nilai sin2x=−1
♠ Menentukan rentang nilai s
sin2x=1→s=11−12sin2xsmaks=11−12.1smaks=11−12=112=2sin2x=−1→s=11−12sin2xsmin=11−12.(−1)smin=11+12=132=23
Sehingga rentang nilai s adalah min<s<maks yaitu 23<s<2
Jadi, nilai s ada pada interval 23<s<2.♡
Nomor 3
Banyaknya akar real f(t)=t9−t adalah ... buah.
♠ Bentuk pemfaktoran :
p2−q2=(p−q)(p+q) atau pn−1=(pn/2−1)(pn/2+1)
dengan n genap
♠ Untuk menentukan akar-akarnya, maka f(t)=0
f(t)=0t9−t=0t(t8−1)=0t(t4−1)(t4+1)=0t(t2−1)(t2+1)(t4+1)=0t(t−1)(t+1)(t2+1)(t4+1)=0
♠ Sehingga akar-akarnya:
t=0,t=1,t=−1 dan t2=−1 (tidak real) serta t4=−1 (tidak real).
Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. ♡
p2−q2=(p−q)(p+q) atau pn−1=(pn/2−1)(pn/2+1)
dengan n genap
♠ Untuk menentukan akar-akarnya, maka f(t)=0
f(t)=0t9−t=0t(t8−1)=0t(t4−1)(t4+1)=0t(t2−1)(t2+1)(t4+1)=0t(t−1)(t+1)(t2+1)(t4+1)=0
♠ Sehingga akar-akarnya:
t=0,t=1,t=−1 dan t2=−1 (tidak real) serta t4=−1 (tidak real).
Jadi, akar-akar realnya ada tiga yaitu 0, 1, dan -1. ♡
Nomor 4
Banyak cara menempatkan 10 kelereng identik ke dalam 5 kotak dengan setiap kotak memuat paling sedikit
1 kelereng adalah ....
♠ Karena kelereng identik, maka yang menentukan urutannya adalah banyaknya kelereng setiap kotak ,
artinya jika isi setiap kotak 2 2 2 2 2 , maka hanya ada satu susunan karena diacak seperti apapun tidak akan berpengaruh
sebab kelerengnya identik . Dan untuk susunan 6 1 1 1 1 akan berbeda dengan 1 6 1 1 1 .
♠ Untuk kasus ini, kita harus menggunakan permutasi berulang.
Konsep permutasi berulang : Banyaknya huruf dibagi dengan huruf yang sama saja.
Misalkan ada kata "BAHAGIA" akan disusun ulang, maka ada 7!3! kata yang diperoleh (banyak huruf ada 7, huruf "A" ada 3 yang sama) . Misalkan lagi ada kata "MATEMATIKA" akan disusun ulang, maka ada 10!2!.3!.2! kata yang diperoleh (banyak huruf ada 10, huruf yang kembar : "M" ada 2, "A" ada 3, "T" ada 2).
Pada kasus ini anggap saja banyaknya kelereng setiap kotak mewakili sebuah huruf, misalkan susunan 6 1 1 1 1 (artinya kotak I ada 6 kelereng, kotak II ada 1 kelereng, kotak III ada 1 kelereng, kotak IV ada 1 kelereng, kotak V ada 1 kelereng) bisa disusun ulang lagi (misalkan 1 6 1 1 1) akan ada 5!4!=5 susunan ( total angka ada 5, angka kembar : angka 1 ada 4 yang kembar).
♠ Menentukan susunan yang mungkin dan banyak caranya dari 10 kelereng yang diletakkan pada 5 kotak dengan setiap kotak memuat paling sedikit 1 kelereng
Kemungkinan I : 6 1 1 1 1 , banyak cara = 5!4!=5
Kemungkinan II : 5 2 1 1 1 , banyak cara = 5!3!=20
Kemungkinan III : 4 3 1 1 1 , banyak cara = 5!3!=20
Kemungkinan IV : 4 2 2 1 1 , banyak cara = 5!2!.2!=30
Kemungkinan V : 3 3 2 1 1 , banyak cara = 5!2!.2!=30
Kemungkinan VI : 3 2 2 2 1 , banyak cara = 5!3!=20
Kemungkinan VII : 2 2 2 2 2 , banyak cara = 5!5!=1
Sehingga total cara = 5 + 20 + 20 + 30 + 30 20 + 1 = 126 cara
Jadi, banyak caranya ada 126 cara. ♡
♠ Untuk kasus ini, kita harus menggunakan permutasi berulang.
Konsep permutasi berulang : Banyaknya huruf dibagi dengan huruf yang sama saja.
Misalkan ada kata "BAHAGIA" akan disusun ulang, maka ada 7!3! kata yang diperoleh (banyak huruf ada 7, huruf "A" ada 3 yang sama) . Misalkan lagi ada kata "MATEMATIKA" akan disusun ulang, maka ada 10!2!.3!.2! kata yang diperoleh (banyak huruf ada 10, huruf yang kembar : "M" ada 2, "A" ada 3, "T" ada 2).
Pada kasus ini anggap saja banyaknya kelereng setiap kotak mewakili sebuah huruf, misalkan susunan 6 1 1 1 1 (artinya kotak I ada 6 kelereng, kotak II ada 1 kelereng, kotak III ada 1 kelereng, kotak IV ada 1 kelereng, kotak V ada 1 kelereng) bisa disusun ulang lagi (misalkan 1 6 1 1 1) akan ada 5!4!=5 susunan ( total angka ada 5, angka kembar : angka 1 ada 4 yang kembar).
♠ Menentukan susunan yang mungkin dan banyak caranya dari 10 kelereng yang diletakkan pada 5 kotak dengan setiap kotak memuat paling sedikit 1 kelereng
Kemungkinan I : 6 1 1 1 1 , banyak cara = 5!4!=5
Kemungkinan II : 5 2 1 1 1 , banyak cara = 5!3!=20
Kemungkinan III : 4 3 1 1 1 , banyak cara = 5!3!=20
Kemungkinan IV : 4 2 2 1 1 , banyak cara = 5!2!.2!=30
Kemungkinan V : 3 3 2 1 1 , banyak cara = 5!2!.2!=30
Kemungkinan VI : 3 2 2 2 1 , banyak cara = 5!3!=20
Kemungkinan VII : 2 2 2 2 2 , banyak cara = 5!5!=1
Sehingga total cara = 5 + 20 + 20 + 30 + 30 20 + 1 = 126 cara
Jadi, banyak caranya ada 126 cara. ♡
Nomor 5
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2p. Titik-titik P, Q, dan R masing-masing adalah titik tengah FB, FG, dan AD.
Luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah .....
♣ Gambar
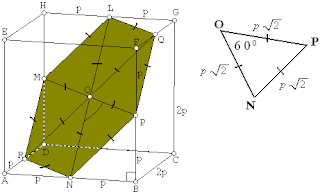
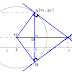
Bidang irisannya adalah bidang NPQLMR berwarna hijau di dalam kubus. Bidang irisannya membentuk segienam beraturan sehingga ada 6 segitiga sama sisi yang menyusunnya, salah satunya segitiga NOP.
Segitiga NBP , panjang
NP=√NB2+BP2=√p2+p2=√2p2=p√2
sehingga panjang NO = OP = NP = p√2 seperti pada gambar di atas
♣ Menentukan luas segitiga NOP
Luas NOP =12.NO.OP.sin60∘=12.p√2.p√2.12√3 Luas NOP =12p2√3
Sehingga luas bidang irisannya :
Luas = 6 × Luas NOP = 6×12p2√3=3p2√3
Jadi, luas bidang irisannya adalah 3p2√3.♡

Bidang irisannya adalah bidang NPQLMR berwarna hijau di dalam kubus. Bidang irisannya membentuk segienam beraturan sehingga ada 6 segitiga sama sisi yang menyusunnya, salah satunya segitiga NOP.
Segitiga NBP , panjang
NP=√NB2+BP2=√p2+p2=√2p2=p√2
sehingga panjang NO = OP = NP = p√2 seperti pada gambar di atas
♣ Menentukan luas segitiga NOP
Luas NOP =12.NO.OP.sin60∘=12.p√2.p√2.12√3 Luas NOP =12p2√3
Sehingga luas bidang irisannya :
Luas = 6 × Luas NOP = 6×12p2√3=3p2√3
Jadi, luas bidang irisannya adalah 3p2√3.♡







Mas Darma. Saya mau nanya, untuk nomor 2 yang dijelaskan nilai minimum dan maksimum saat penyebutnya itu maksimum dan minimum itu maksudnya apa ya mas? Materi yang mana? Mohon jika ada linknya di blog KoMa mas. Terima kasih mas. Saya baru tahu nilai turunan fungsi seperti ini.
BalasHapusHallow dek deny.
Hapusuntuk nilai maksimum dan minimum suatu fungsi trigonometri bisa dibaca pada artikel fungsi trigonometri .
Bentuk s=11−12sin2x
Hapusadalah bentuk pecahan dengan pembilangnya konstanta yaitu 1 dan penyebutnya 1−12sin2x . Karena bentuk pecahan dan pembilangnya sudah pasti tetap nilainya, maka nilai maksimum atau minimum s bergantung dari nilai penyebutnya.
Misalkan bentuk pecahan f=1a , nilai f akan minimum (sekecil mungkin) jika nilai a (penyebutnya) maksimum (sebesar mungkin), begitu juga sebaliknya. Misalkan nilai a berkisar : 2≤a≤5 artinya nilai minimum a adalah 2 dan maksimum a adalah 5. Sehingga :
nilai f maksimum =12
dan nilai f minimum =15.
seperti itu maksudnya pembahasan soal nomor 2.
Catatan : sebenarnya bisa menggunakan konsep turunan juga untuk mencari nilai maksimum atau minimum fungsi trigonometri, tapi akan lebih ribet nantinya.
Oh begitu saya mengerti mas. Jadi sebenarnya nilai maksimum dan minimum ini gak ada hubungannya dengan nilai maksimum/min dari turunan nya ya mas?
HapusSaya akan terus baca teori-teori nya mas, ternyata banyak konsep dasar yang sering saya lupakan, justru berguna saat soal-soal tingkat yang lebih tinggi seperti seleksi PTN ini ya. Terima kasih mas.
OK dek. Tetap semangat terus belajarnya.
HapusTerimakasih. Sangat bermanfaat ilmunya
BalasHapusHallow @Haris,
HapusTerimakasih untuk kunjungannya ke blog dunia-informa ini.
semoga terus bisa bermanfaat.
halo mas darma,saya mau tanya kenapa kemungkinan susunan yang terjadi hanya 7 ? bukankah 61111 dan 11611 beda ?
BalasHapushallow @alwan,
Hapusterimakasih untuk kunjungannya ke blog dunia-informa ini.
untuk bentuk 61111 berbeda dengan 11611, dimana kalau diacak ada 5 kemungkinan yaitu 61111, 16111, 11611, 11161, dan 11116. untuk memudahkan penghitungan, kita gunakan permutasi berulang seperti pembahasan di atas agar kita tidak secara manual mendata satu persatu.
seperti itu penjelasannya.
semoga terus bisa membantu.
terimakasih mas
BalasHapus