Nomor 1
Penyelesaian pertidaksamaan x2+x−6x−2≥0 adalah ....
♣ Menentukan nilai x
x2+x−6x−2≥0(x−2)(x+3)x−2≥0x=2∨x=−3
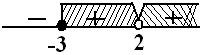
Jadi, solusinya adalah HP={−3≤x<2∨x>2}.♡
x2+x−6x−2≥0(x−2)(x+3)x−2≥0x=2∨x=−3

Jadi, solusinya adalah HP={−3≤x<2∨x>2}.♡
Nomor 2
Deret aritmetika terdiri atas 10 suku dengan suku pertama 4 dan jumlah 10 suku pertamanya adalah 130. Suku yang terakhir deret
tersebut adalah ....
♠ Barisan aritmetika : Un=a+(n−1)b dan Sn=n2(2a+(n−1)b)
♠ Menentukan nilai b dengan a=4
S10=130102(2a+(10−1)b)=1305(2.4+9b)=130(bagi 5)8+9b=269b=26−89b=18→b=2
♠ Menentukan suku terakhir (U10)
U10=a+9b=4+9.2=4+18=22
Jadi, suku terakhirnya adalah 22. ♡
♠ Menentukan nilai b dengan a=4
S10=130102(2a+(10−1)b)=1305(2.4+9b)=130(bagi 5)8+9b=269b=26−89b=18→b=2
♠ Menentukan suku terakhir (U10)
U10=a+9b=4+9.2=4+18=22
Jadi, suku terakhirnya adalah 22. ♡
Cara II
♠ Barisan aritmetika : Sn=n2(a+Un)
♠ Menentukan suku terakhir (U10)
S10=130102(a+U10)=1305(4+U10)=130(bagi 5)4+U10=26U10=26−4=22
Jadi, suku terakhirnya adalah 22. ♡
♠ Barisan aritmetika : Sn=n2(a+Un)
♠ Menentukan suku terakhir (U10)
S10=130102(a+U10)=1305(4+U10)=130(bagi 5)4+U10=26U10=26−4=22
Jadi, suku terakhirnya adalah 22. ♡
Nomor 3
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik A ke bidang BDE adalah ....
♣ Gambar

Panjang EP=√AP2+AE2=√(3√2)2+62=3√6
Jarak A ke BDE sama dengan jarak A ke EP yaitu panjang AM.
♣ Menentukan panjang AM dengan luas segitiga
LuasΔAEP(alasnya AP)=LuasΔAEP(alasnya EP)12.AP.EA=12.EP.AMAP.EA=EP.AMAM=AP.EAEPAM=6.3√23√6AM=2√3
Jadi, jarak A ke BDE adalah 2√3.♡

Panjang EP=√AP2+AE2=√(3√2)2+62=3√6
Jarak A ke BDE sama dengan jarak A ke EP yaitu panjang AM.
♣ Menentukan panjang AM dengan luas segitiga
LuasΔAEP(alasnya AP)=LuasΔAEP(alasnya EP)12.AP.EA=12.EP.AMAP.EA=EP.AMAM=AP.EAEPAM=6.3√23√6AM=2√3
Jadi, jarak A ke BDE adalah 2√3.♡
Cara II
♣ Gambar

Pada gambar di atas, terlihat bahwa AG dibagi menjadi tiga bagian yaitu AM, MK, dan KG , sehingga jarak A ke BDE sama dengan 13AG
AM=13AG=13.6√3=2√3
Jadi, jarak A ke BDE adalah 2√3.♡
♣ Gambar

Pada gambar di atas, terlihat bahwa AG dibagi menjadi tiga bagian yaitu AM, MK, dan KG , sehingga jarak A ke BDE sama dengan 13AG
AM=13AG=13.6√3=2√3
Jadi, jarak A ke BDE adalah 2√3.♡
Nomor 4
Bentuk sederhana tan2x+cos2xsinx+secx adalah ....
♠ Konsep dasar :
Identitas : cos2x=1−sin2x dan tan2x=sec2x−1
Pemfaktoran : p2−q2=(p+q)(p−q)
♠ Menyederhanakan soal
tan2x+cos2xsinx+secx=(sec2x−1)+(1−sin2x)(secx+sinx)=sec2x−sin2x(secx+sinx)=(secx+sinx).(secx−sinx)(secx+sinx)=secx−sinx
Jadi, bentuk sederhananya adalah secx−sinx.♡
Identitas : cos2x=1−sin2x dan tan2x=sec2x−1
Pemfaktoran : p2−q2=(p+q)(p−q)
♠ Menyederhanakan soal
tan2x+cos2xsinx+secx=(sec2x−1)+(1−sin2x)(secx+sinx)=sec2x−sin2x(secx+sinx)=(secx+sinx).(secx−sinx)(secx+sinx)=secx−sinx
Jadi, bentuk sederhananya adalah secx−sinx.♡
Nomor 5
Diketahui premis-premis :
* Jika saya minum kopi, saya tidak dapat tidur
* Saya tidur atau saya merasa pusing
* Saya minum kopi
Kesimpulan yang sah adalah ....
* Jika saya minum kopi, saya tidak dapat tidur
* Saya tidur atau saya merasa pusing
* Saya minum kopi
Kesimpulan yang sah adalah ....
♣ Menarik kesimpulan :
Silogisme : p→qq→r∴p→r Modus ponens : p→qp∴q
♣ Mengubah premis-premis menjadi simbol matematika:
1). Jika saya minum kopi⏟p, maka saya tidak dapat tidur⏟∼q.
ditulis : p→∼q
2). Saya tidur⏟q atau saya merasa pusing⏟r.
ditulis : q∨r setara dengan ∼q→r
3). saya minum kopi⏟p . ditulis : p
♣ Menarik kesimpulan dari premis-premis 1) , 2), dan 3):
Silogisme 1) dan 2): p→∼q∼q→r∴p→r Modus ponens dengan 3): p→rp∴r
Jadi, kesimpulannya adalah r dibaca : saya merasa pusing. ♡
Catatan : Tidak ada pilihan jawaban yang sesuai.
Silogisme : p→qq→r∴p→r Modus ponens : p→qp∴q
♣ Mengubah premis-premis menjadi simbol matematika:
1). Jika saya minum kopi⏟p, maka saya tidak dapat tidur⏟∼q.
ditulis : p→∼q
2). Saya tidur⏟q atau saya merasa pusing⏟r.
ditulis : q∨r setara dengan ∼q→r
3). saya minum kopi⏟p . ditulis : p
♣ Menarik kesimpulan dari premis-premis 1) , 2), dan 3):
Silogisme 1) dan 2): p→∼q∼q→r∴p→r Modus ponens dengan 3): p→rp∴r
Jadi, kesimpulannya adalah r dibaca : saya merasa pusing. ♡
Catatan : Tidak ada pilihan jawaban yang sesuai.
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.