Nomor 11
Diketahui f(x)=ax2+bx+4 . Jika gradien garis singgung kurva di x=2 adalah −1 dan di x=1 adalah 3,
maka a+b=....
♠ Konsep Dasar Gradien (m) garis singgung : m=f′(x)
f(x)=ax2+bx+4→f′(x)=2ax+b
♠ Substitusi semua gradiennya dengan f′(x)=2ax+b
* m=−1 saat x=2 substitusi ke m=f′(x)
−1=f′(2)→−1=2a.2+b→4a+b=−1 ...pers(i)
* m=3 saat x=1 substitusi ke m=f′(x)
3=f′(1)→3=2a.1+b→2a+b=3 ...pers(ii)
♠ Eliminasi pers(i) dan pers(ii)
4a+b=−12a+b=3−2a=−4a=−2
pers(ii) : 2a+b=3→2.(−2)+b=3→b=7
Sehingga : a+b=−2+7=5
Jadi, nilai a+b=5.♡
f(x)=ax2+bx+4→f′(x)=2ax+b
♠ Substitusi semua gradiennya dengan f′(x)=2ax+b
* m=−1 saat x=2 substitusi ke m=f′(x)
−1=f′(2)→−1=2a.2+b→4a+b=−1 ...pers(i)
* m=3 saat x=1 substitusi ke m=f′(x)
3=f′(1)→3=2a.1+b→2a+b=3 ...pers(ii)
♠ Eliminasi pers(i) dan pers(ii)
4a+b=−12a+b=3−2a=−4a=−2
pers(ii) : 2a+b=3→2.(−2)+b=3→b=7
Sehingga : a+b=−2+7=5
Jadi, nilai a+b=5.♡
Nomor 12
Jika f(x)=1√x , maka −2f′(x)=....
♣ Rumus dasar Turunan : y=xn→y′=nxn−1
♣ Menentukan turunan fungsi
f(x)=1√xf(x)=x−12f′(x)=−12x−12−1=−12x−32=−121x32f′(x)=−121x√x
Sehingga : −2f′(x)=−2.−121x√x=1x√x
Jadi, nilai −2f′(x)=1x√x.♡
♣ Menentukan turunan fungsi
f(x)=1√xf(x)=x−12f′(x)=−12x−12−1=−12x−32=−121x32f′(x)=−121x√x
Sehingga : −2f′(x)=−2.−121x√x=1x√x
Jadi, nilai −2f′(x)=1x√x.♡
Nomor 13
Nilai - nilai yang memenuhi pertaksamaan 2x−13x+2≥2 adalah ....
♠ Menyelesaikan pertidaksamaan
2x−13x+2≥22x−13x+2−2≥02x−13x+2−2(3x+2)3x+2≥0−4x−53x+2≥0x=−54∨x=−23
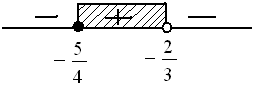
Catatan : Akar - akar penyebut tidak diikutkan (pasti bolong)
Jadi, solusinya adalah HP={−54≤x<−23}.♡
2x−13x+2≥22x−13x+2−2≥02x−13x+2−2(3x+2)3x+2≥0−4x−53x+2≥0x=−54∨x=−23

Catatan : Akar - akar penyebut tidak diikutkan (pasti bolong)
Jadi, solusinya adalah HP={−54≤x<−23}.♡
Nomor 14
Deret S4=U1+U2+U3+U4 merupakan deret aritmetika dan U1>U2. Jika determinan matriks
(U1U2U3U4) adalah −2 dan S4=2,
maka (U1U2U3U4)−1=....
♣ Barisan Aritmetika : Un=a+(n−1)b dan Sn=n2(2a+(n−1)b)
karena U1>U2 , maka bedanya negatif (b<0 ) .
♣ Menentukan determinan
|U1U2U3U4|=−2U1.U4−U2.U3=−2a.(a+3b)−(a+b).(a+2b)=−2a2+3ab−(a2+3ab+2b2)=−2−2b2=−2b2=1→b=±1
yang memenuhi adalah b=−1 karena harus negatif
♣ Menentukan nilai a dari S4=2
S4=2→42(2a+3b)=2→2(2a+3.(−1))=2→a=2
♣ Menentukan matriksnya
A=(U1U2U3U4)=(aa+ba+2ba+3b)
A=(22+(−1)2+2.(−1)2+3.(−1))=(210−1)
♣ Menentukan Invers matriksnya
Konsep Invers : A=(abcd)→A−1=1ad−bc(d−b−ca)
A=(210−1)→A−1=1ad−bc(d−b−ca)A−1=1(−1.2)−(0.(−1))(−1−102)=1−2(−1−102)=(12120−1)
Jadi, inversnya adalah (12120−1).♡
karena U1>U2 , maka bedanya negatif (b<0 ) .
♣ Menentukan determinan
|U1U2U3U4|=−2U1.U4−U2.U3=−2a.(a+3b)−(a+b).(a+2b)=−2a2+3ab−(a2+3ab+2b2)=−2−2b2=−2b2=1→b=±1
yang memenuhi adalah b=−1 karena harus negatif
♣ Menentukan nilai a dari S4=2
S4=2→42(2a+3b)=2→2(2a+3.(−1))=2→a=2
♣ Menentukan matriksnya
A=(U1U2U3U4)=(aa+ba+2ba+3b)
A=(22+(−1)2+2.(−1)2+3.(−1))=(210−1)
♣ Menentukan Invers matriksnya
Konsep Invers : A=(abcd)→A−1=1ad−bc(d−b−ca)
A=(210−1)→A−1=1ad−bc(d−b−ca)A−1=1(−1.2)−(0.(−1))(−1−102)=1−2(−1−102)=(12120−1)
Jadi, inversnya adalah (12120−1).♡
Nomor 15
Panjang sisi miring suatu segitiga siku - siku adalah 2x+2 . Jika panjang dua sisi yang lain adalah 4 dan 22x+1
, maka nilai x yang memenuhi terletak pada interval ....
♠ Gambar
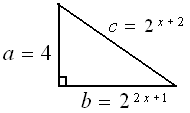
♠ Menentukan interval x dengan c>a dan c>b
c>a2x+2>42x+2>22x+2>2x>0...(HP1) c>b2x+2>22x+1x+2>2x1−x>−1x<1...(HP2)
Sehingga solusinya : HP = HP1∩HP2={0<x<1}
Jadi, interval nilai x adalah {0<x<1}.♡
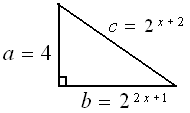
♠ Menentukan interval x dengan c>a dan c>b
c>a2x+2>42x+2>22x+2>2x>0...(HP1) c>b2x+2>22x+1x+2>2x1−x>−1x<1...(HP2)
Sehingga solusinya : HP = HP1∩HP2={0<x<1}
Jadi, interval nilai x adalah {0<x<1}.♡
Cara II :
♠ Gambar
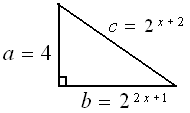
♠ Berdasarkan gambar, berlaku pythagoras yaitu :
Misalkan : 22x=p
a2+b2=c242+(22x+1)2=(2x+2)216+24x+2=22x+416+22.24x=24.22x16+4.(22x)2=16.22x(bagi 4)4+(22x)2=4.22x(ganti p)4+p2=4pp2−4p+4=0(p−2)2=0p=2
nilai x :
p=2→22x=2→2x=1→x=12.
Sehingga nilai a ada pada interval {0<x<1}
Jadi, nilai x ada pada interval {0<x<1}.♡
♠ Gambar
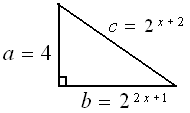
♠ Berdasarkan gambar, berlaku pythagoras yaitu :
Misalkan : 22x=p
a2+b2=c242+(22x+1)2=(2x+2)216+24x+2=22x+416+22.24x=24.22x16+4.(22x)2=16.22x(bagi 4)4+(22x)2=4.22x(ganti p)4+p2=4pp2−4p+4=0(p−2)2=0p=2
nilai x :
p=2→22x=2→2x=1→x=12.
Sehingga nilai a ada pada interval {0<x<1}
Jadi, nilai x ada pada interval {0<x<1}.♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.