Nomor 6
Himpunan penyelesaian pertidaksamaan x−1x<2 adalah ....
♠ Menyelesaikan pertidaksamaan
x−1x<2x−1x−2<0x−1x−2xx<0(x−1)−(2x)x<0−x−1x<0−x−1=0→x=−1x=0
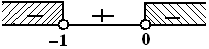
Jadi, solusinya HP={x<−1∨x>0}.♡
x−1x<2x−1x−2<0x−1x−2xx<0(x−1)−(2x)x<0−x−1x<0−x−1=0→x=−1x=0
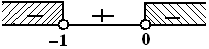
Jadi, solusinya HP={x<−1∨x>0}.♡
Nomor 7
Diketahui suatu fungsi f bersifat f(−x)=−f(x) untuk setiap bilangan real x.
Jika f(3)=−5 dan f(−5)=1, maka f(f(−3))=....
♣ Diketahui f(−x)=−f(x) ....pers(i)
berlaku juga : f(x)=−f(−x) ....pers(ii)
♣ Diketahui nilai : f(3)=−5 dan f(−5)=1
f(−3)=−f(3)=−(−5)=5 ....dari pers(i)
f(5)=−f(−5)=−(1)=−1 ....dari pers(ii)
♣ Menentukan hasilnya
f(f(−3))=f(5)....[ dengan f(−3)=5]=−1
Jadi, nilai f(f(−3))=−1.♡
berlaku juga : f(x)=−f(−x) ....pers(ii)
♣ Diketahui nilai : f(3)=−5 dan f(−5)=1
f(−3)=−f(3)=−(−5)=5 ....dari pers(i)
f(5)=−f(−5)=−(1)=−1 ....dari pers(ii)
♣ Menentukan hasilnya
f(f(−3))=f(5)....[ dengan f(−3)=5]=−1
Jadi, nilai f(f(−3))=−1.♡
Nomor 8
Diketahui sistem persamaan
{x+22−x−y3=1,x+y3−y+12=2.
Nilai x+y adalah ....
Nilai x+y adalah ....
♠ Menyederhanakan sistem persamaan
x+22−x−y3=1(kali 6)3(x+2)−2(x−y)=6x+2y=0....pers(i)x+y3−y+12=2(kali 6)2(x+y)−3(y+1)=122x−y=15....pers(ii)
♠ Eliminasi pers(i) dan pers(ii)
x+2y=0×1x+2y=02x−y=15×24x−2y=30+5x=30x=6
pers(i) : x+2y=0→6+2y=0→y=−3
Sehingga nilai x+y=6+(−3)=3
Jadi, nilai x+y=3.♡
x+22−x−y3=1(kali 6)3(x+2)−2(x−y)=6x+2y=0....pers(i)x+y3−y+12=2(kali 6)2(x+y)−3(y+1)=122x−y=15....pers(ii)
♠ Eliminasi pers(i) dan pers(ii)
x+2y=0×1x+2y=02x−y=15×24x−2y=30+5x=30x=6
pers(i) : x+2y=0→6+2y=0→y=−3
Sehingga nilai x+y=6+(−3)=3
Jadi, nilai x+y=3.♡
Nomor 9
Empat orang siswa akan mengikuti suatu perlombaan karya inovatif. Untuk itu, diperlukan biaya Rp 900.000,00.
Karena masing-masing memiliki kondisi keuangan yang berbeda, besar kontribusi masing-masing siswa tidak sama.
Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya. Siswa B memberikan kontribusi
sepertiga dari jumlah kontribusi tiga siswa lainnya. Siswa C memberikan kontribusi seperempat dari jumlah kontribusi
tiga siswa lainnya. Besar kontribusi siswa D adalah Rp ....
♣ Menyusun persamaan
A=12(B+C+D)→2A=B+C+D....pers(i)B=13(A+C+D)→3B=A+C+D....pers(ii)C=14(A+B+D)→4C=A+B+D....pers(iii)A+B+C+D=900.000....pers(iv)
♣ Substitusi pers(iv) ke semua persamaan
pers(i) : 2A=B+C+D2A=900.000−A3A=900.000A=300.000pers(ii) : 3B=A+C+D3B=900.000−B4B=900.000B=225.000pers(iii) : 4C=A+B+D4C=900.000−C5C=900.000C=180.000
♣ Menentukan nilai D
A+B+C+D=900.000300.000+225.000+180.000+D=900.000D=195.000
Jadi, besarnya kontribusi siswa D adalah Rp 195.000,00. ♡
A=12(B+C+D)→2A=B+C+D....pers(i)B=13(A+C+D)→3B=A+C+D....pers(ii)C=14(A+B+D)→4C=A+B+D....pers(iii)A+B+C+D=900.000....pers(iv)
♣ Substitusi pers(iv) ke semua persamaan
pers(i) : 2A=B+C+D2A=900.000−A3A=900.000A=300.000pers(ii) : 3B=A+C+D3B=900.000−B4B=900.000B=225.000pers(iii) : 4C=A+B+D4C=900.000−C5C=900.000C=180.000
♣ Menentukan nilai D
A+B+C+D=900.000300.000+225.000+180.000+D=900.000D=195.000
Jadi, besarnya kontribusi siswa D adalah Rp 195.000,00. ♡
Nomor 10
Jika f(2x+4)=2−x2, maka f−1(x)=....
♠ Konsep invers : f(A)=B⇔f−1(B)=A
sehingga : f(2x+4)=2−x2⇒f−1(2−x2)=2x+4
♠ Menentukan inversnya
Misal : p=2−x2→x=2(2−p)=4−2p
Substitusi bentuk p
f−1(2−x2)=2x+4f−1(p)=2(4−2p)+4f−1(p)=12−4p
Sehingga diperoleh : f−1(x)=12−4x
Jadi, diperoleh f−1(x)=12−4x.♡
sehingga : f(2x+4)=2−x2⇒f−1(2−x2)=2x+4
♠ Menentukan inversnya
Misal : p=2−x2→x=2(2−p)=4−2p
Substitusi bentuk p
f−1(2−x2)=2x+4f−1(p)=2(4−2p)+4f−1(p)=12−4p
Sehingga diperoleh : f−1(x)=12−4x
Jadi, diperoleh f−1(x)=12−4x.♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.