Nomor 11
Jika A=[21a4]
merupakan matriks yang mempunyai invers dan det(B)=4, maka hasil kali semua nilai a yang mungkin sehingga
det(A)=16det((AB)−1)
adalah .....
♠ sifat-sifat determinan
|A−1|=1|A| dan |A.B|=|A|.|B|
♠ Menentukan nilai determinan A
A=[21a4]
det(A)=|A|=2.4−a.1=8−a
Diketahui juga : det(B)=|B|=4
♠ Menentukan nilai a
det(A)=16det((AB)−1)|A|=16|(AB)−1||A|=16.1|AB||A|=16|A|.|B||A|2=16|B|(8−a)2=164(8−a)2=464−16a+a2=4a2−16a+60=0(a−6)(a−10)=0a1=6∨a2=10
hasil kali nilai a adalah a1.a2=6.10=60
atau gunakan operasi akar-akar :
a2−16a+60=0→a1.a2=ca=601=60
Jadi, hasil kali semua nilai a adalah 60. ♡
|A−1|=1|A| dan |A.B|=|A|.|B|
♠ Menentukan nilai determinan A
A=[21a4]
det(A)=|A|=2.4−a.1=8−a
Diketahui juga : det(B)=|B|=4
♠ Menentukan nilai a
det(A)=16det((AB)−1)|A|=16|(AB)−1||A|=16.1|AB||A|=16|A|.|B||A|2=16|B|(8−a)2=164(8−a)2=464−16a+a2=4a2−16a+60=0(a−6)(a−10)=0a1=6∨a2=10
hasil kali nilai a adalah a1.a2=6.10=60
atau gunakan operasi akar-akar :
a2−16a+60=0→a1.a2=ca=601=60
Jadi, hasil kali semua nilai a adalah 60. ♡
Nomor 12
Jika semua akar persamaan x2−px+12=0 merupakan bilangan bulat positif, maka jumlah semua nilai p
yang mungkin adalah .....
♣ Persamaan kuadrat : x2−px+12=0
a=1,b=−p, dan c=12
♣ Operasi akar-akar :
x1+x2=−ba=−(−p)1=p ....pers(i)
x1.x2=ca=121=12 ....pers(ii)
♣ Menentukan nilai p dari pers(i) dan pers(ii) dengan x1 dan x2 bilangan bulat positif.
x1+x2=p dan x1.x2=12
*). x1=1,x2=12→p=x1+x2=1+12=13
*). x1=2,x2=6→p=x1+x2=2+6=8
*). x1=3,x2=4→p=x1+x2=3+4=7
Sehingga jumlah semua nilai p yang mungkin :
Jumlah = 13 + 8 + 7 = 28.
Jadi, jumlah semua nilai p adalah 28. ♡
a=1,b=−p, dan c=12
♣ Operasi akar-akar :
x1+x2=−ba=−(−p)1=p ....pers(i)
x1.x2=ca=121=12 ....pers(ii)
♣ Menentukan nilai p dari pers(i) dan pers(ii) dengan x1 dan x2 bilangan bulat positif.
x1+x2=p dan x1.x2=12
*). x1=1,x2=12→p=x1+x2=1+12=13
*). x1=2,x2=6→p=x1+x2=2+6=8
*). x1=3,x2=4→p=x1+x2=3+4=7
Sehingga jumlah semua nilai p yang mungkin :
Jumlah = 13 + 8 + 7 = 28.
Jadi, jumlah semua nilai p adalah 28. ♡
Nomor 13
Jika garis g sejajar dengan garis y=2+x dan menyinggung kurva y=x2−3x+3, maka garis g
memotong sumbu-Y di titik ....
♠ Konsep Dasar
*). garis y=ax+b→ gradiennya : m=a
*). dua garis sejajar, maka gradiennya sama.
*). Persamaan garis singgung (PGS) di titik (x1,y1) dan menyinggung kurva y=f(x) , persamaannya : y−y1=m(x−x1) dengan gradien m=f′(x)
♠ Garis g sejajar dengan garis y=2+x, artinya gradiennya sama
y=x+2→mg=1
♠ garis g menyinggung kurva y=x2−3x+3, sehingga gradiennya : mg=f′(x)
mg=f′(x)1=2x−3x=2
♠ Substitusi x=2 ke kurva untuk menentukan titik singgungnya
x=2→y=x2−3x+3y=22−3.2+3y=1
titik singgungnya : (x1,y1)=(2,1)
♠ Menentukan PGS nya
y−y1=m(x−x1)y−1=1(x−2)y=x−1
sehingga garis g:y=x−1
♠ Menentukan titik potong garis g pada sumbu Y dengan substitusi x=0
x=0→y=x−1y=0−1=−1
Jadi, garis g memeotong sumbu Y di titik (0,−1).♡
*). garis y=ax+b→ gradiennya : m=a
*). dua garis sejajar, maka gradiennya sama.
*). Persamaan garis singgung (PGS) di titik (x1,y1) dan menyinggung kurva y=f(x) , persamaannya : y−y1=m(x−x1) dengan gradien m=f′(x)
♠ Garis g sejajar dengan garis y=2+x, artinya gradiennya sama
y=x+2→mg=1
♠ garis g menyinggung kurva y=x2−3x+3, sehingga gradiennya : mg=f′(x)
mg=f′(x)1=2x−3x=2
♠ Substitusi x=2 ke kurva untuk menentukan titik singgungnya
x=2→y=x2−3x+3y=22−3.2+3y=1
titik singgungnya : (x1,y1)=(2,1)
♠ Menentukan PGS nya
y−y1=m(x−x1)y−1=1(x−2)y=x−1
sehingga garis g:y=x−1
♠ Menentukan titik potong garis g pada sumbu Y dengan substitusi x=0
x=0→y=x−1y=0−1=−1
Jadi, garis g memeotong sumbu Y di titik (0,−1).♡
Nomor 14
Diketahui median dari 11 nilai pengamatan adalah 10, sedangkan rata-rata dari nilai pengamatan yang lebih kecil daripada median
adalah 4. Jika rata-rata dari 11 nilai pengamatan tersebut sama dengan dua kali median, maka rata-rata nilai pengamatan yang lebih besar
daripada median adalah ....
♣ Konsep rata-rata gabungan (¯Xgb)
¯Xgb=n1¯X1+n2¯X2+n3¯X3n1+n2+n3
Keterangan :
¯Xgb= rata - rata gabungan
¯X1= rata - rata kelompok I
n1= banyak anggota kelompok I
♣ Data dibagi menjadi tiga kelompok
*). Kelompok I : data sebelum median ada 5 data dengan rata-rata 4, artinya n1=5 dan ¯X1=4
*). Kelompok II : mediannya itu sendiri, ada 1 data dengan nilai 10, artinya n2=1 dan ¯X2=10
*). Kelompok III : data setelah median ada 5 data dengan rata-rata misalkan a , artinya n3=5 dan ¯X3=a
*). rata-rata gabungan = dua kali median
¯Xgb=2×10=20
♣ Menentukan nilai a
¯Xgb=n1¯X1+n2¯X2+n3¯X3n1+n2+n320=5.4+1.10+5.a5+1+520=20+10+5a11220=30+5a5a=190a=38
Jadi, rata-rata nilai pengamatan lebih besar daripada median adalah 38. ♡
¯Xgb=n1¯X1+n2¯X2+n3¯X3n1+n2+n3
Keterangan :
¯Xgb= rata - rata gabungan
¯X1= rata - rata kelompok I
n1= banyak anggota kelompok I
♣ Data dibagi menjadi tiga kelompok
*). Kelompok I : data sebelum median ada 5 data dengan rata-rata 4, artinya n1=5 dan ¯X1=4
*). Kelompok II : mediannya itu sendiri, ada 1 data dengan nilai 10, artinya n2=1 dan ¯X2=10
*). Kelompok III : data setelah median ada 5 data dengan rata-rata misalkan a , artinya n3=5 dan ¯X3=a
*). rata-rata gabungan = dua kali median
¯Xgb=2×10=20
♣ Menentukan nilai a
¯Xgb=n1¯X1+n2¯X2+n3¯X3n1+n2+n320=5.4+1.10+5.a5+1+520=20+10+5a11220=30+5a5a=190a=38
Jadi, rata-rata nilai pengamatan lebih besar daripada median adalah 38. ♡
Nomor 15
Empat buku berjudul Matematika dan dua buku berjudul Biologi akan disusun dilemari buku dalam satu baris. Misalkan A adalah
kejadian susunan buku sehingga tidak ada tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Jika buku dengan judul
yang sama tidak dibedakan, maka peluang kejadian A adalah ....
♠ Pada kasus ini menggunakan Permutasi Berulang.
Misalkan kata "BAHAGIA" akan disusun ulang, maka banyaknya kata baru (tidak harus bermakna) yang diperoleh adalah total hurufhuruf yang sama=7!3!=7×6×5×4 kata, di sini huruf yang sama hanya huruf A sebanyak 3.
Contoh lain, kata "MATEMATIKA" disusun ulang, kata baru sebanyak 10!2!×3!×2! kata (total huruf = 10, yang sama : M = 2, A = 3, T = 2).
♠ Konsep peluang
P(A)=n(A)n(S)
pada soal ini kita misalkan :
A= kejadian tidak terdapat tiga atau lebih buku tersusun berurutan.
♠ Misal : M = Matematika dan B = Biologi
Ada 4M 2B , artinya n(S)=6!4!.21=3.5=15
n(S) adalah ruang sampel (semua susunan yang mungkin)
♠ Menentukan n(A)
Agar tidak terdapat tiga atau lebih buku yang sama tersusun berurutan, kita kelompokkan menjadi lima bagian dengan tiga kemungkinan, yaitu :
*). Kemungkinan I :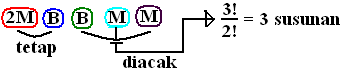
KI = 3!2!=3 susunan : MMBBMM, MMBMBM, MMBMMB
*). Kemungkinan II :
ada 3!2!=3 susunan : MMBBMM, MBMBMM, BMMBMM
hanya saja ada satu susunan buku (MMBBMM) sudah ada pada kemungkinan I,
sehingga, KII = 3 - 1 = 2 susunan
*). Kemungkinan III , 2M ada ditengah yaitu : MBMMBM
diperoleh KIII = 1 susunan
Sehingga semua kemungkinan kejadian A :
n(A)=KI+KII+KIII=3+2+1=6
♠ Menentukan peluangnya
P(A)=n(A)n(S)=615=25
Jadi, peluang tidak terdapat tiga atau lebih buku yang sama tersusun berurutan adalah 25.♡
Keterangan kemungkinan yang ada :
Kemungkinan I :

*). Kita bagi menjadi 5 kelompok yaitu 2M, B, B, M, dan M dengan 2M dan B posisinya pasti tetap di depan.
*). Tiga kelompok terakhir (B, M, M) kita acak posisinya dengan banyak susunan 3!2!=3 cara.
Sehingga semua susunan kemungkinan I ada 3!2!=3 cara yaitu MMBBMM, MMBMBM, dan MMBMMB
Hal yang sama juga untuk kemungkinan II, hanya saja B dan 2M posisinya tetap dibelakang.
Misalkan kata "BAHAGIA" akan disusun ulang, maka banyaknya kata baru (tidak harus bermakna) yang diperoleh adalah total hurufhuruf yang sama=7!3!=7×6×5×4 kata, di sini huruf yang sama hanya huruf A sebanyak 3.
Contoh lain, kata "MATEMATIKA" disusun ulang, kata baru sebanyak 10!2!×3!×2! kata (total huruf = 10, yang sama : M = 2, A = 3, T = 2).
♠ Konsep peluang
P(A)=n(A)n(S)
pada soal ini kita misalkan :
A= kejadian tidak terdapat tiga atau lebih buku tersusun berurutan.
♠ Misal : M = Matematika dan B = Biologi
Ada 4M 2B , artinya n(S)=6!4!.21=3.5=15
n(S) adalah ruang sampel (semua susunan yang mungkin)
♠ Menentukan n(A)
Agar tidak terdapat tiga atau lebih buku yang sama tersusun berurutan, kita kelompokkan menjadi lima bagian dengan tiga kemungkinan, yaitu :
*). Kemungkinan I :

KI = 3!2!=3 susunan : MMBBMM, MMBMBM, MMBMMB
*). Kemungkinan II :

ada 3!2!=3 susunan : MMBBMM, MBMBMM, BMMBMM
hanya saja ada satu susunan buku (MMBBMM) sudah ada pada kemungkinan I,
sehingga, KII = 3 - 1 = 2 susunan
*). Kemungkinan III , 2M ada ditengah yaitu : MBMMBM
diperoleh KIII = 1 susunan
Sehingga semua kemungkinan kejadian A :
n(A)=KI+KII+KIII=3+2+1=6
♠ Menentukan peluangnya
P(A)=n(A)n(S)=615=25
Jadi, peluang tidak terdapat tiga atau lebih buku yang sama tersusun berurutan adalah 25.♡
Keterangan kemungkinan yang ada :
Kemungkinan I :

*). Kita bagi menjadi 5 kelompok yaitu 2M, B, B, M, dan M dengan 2M dan B posisinya pasti tetap di depan.
*). Tiga kelompok terakhir (B, M, M) kita acak posisinya dengan banyak susunan 3!2!=3 cara.
Sehingga semua susunan kemungkinan I ada 3!2!=3 cara yaitu MMBBMM, MMBMBM, dan MMBMMB
Hal yang sama juga untuk kemungkinan II, hanya saja B dan 2M posisinya tetap dibelakang.
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.