Pembahasan Soal SPMK UB Matematika IPA Kode 96 tahun 2010 nomor 6 sampai 10

Nomor 6

Grafik fungsi kuadrat

$y = ax^2 + bx + c \,$ melalui titik (5,0) , (10,0) , dan (0,10). Jika titik minimum fungsi dicapai di titik

$( x_0 , y_0) \,$ , maka

$x_0 + y_0 \,$ adalah ....

$\spadesuit \,$ Konsep Dasar
*) Menyusun FK melalui tipot sumbu X di (

$x_1,0$ ) dan (

$x_2,0$ )
FK :

$y = a(x-x_1)(x-x_2)$
*) Titik puncaknya (

$x_p,y_p$ ) :

$x_p = \frac{-b}{2a} \,$ dan

$y_p = \frac{D}{-4a} \,$ dengan

$D = b^2 - 4ac$

$\spadesuit \,$ Menyusun FK melalu titik (5,0) dan (10,0) artinya

$x_1 = 5 \,$ dan

$x_2 = 10$
FK :

$y = a(x-x_1)(x-x_2) \rightarrow y = a(x-5)(x-10)$

$\spadesuit \,$ Substitusi titik (0,10) ke FK

$\begin{align} (x,y) = (0,10) \rightarrow y & = a(x-5)(x-10) \\ 10 & = a(0-5)(0-10) \\ 10 & = a(-5)(-10) \\ 10 & = 50a \\ a & = \frac{10}{50} = \frac{1}{5} \end{align}$
FK menjadi :

$y = a(x-5)(x-10) = \frac{1}{5}(x-5)(x-10)$

$y = \frac{1}{5}x^2 - 3x + 10$

$\spadesuit \,$ Menentukan titik puncak

$(x_p,y_p) = (x_0,y_0)$
FK :

$y = \frac{1}{5}x^2 - 3x + 10 \rightarrow a = \frac{1}{5}, \, b = -3, \, c = 10$

$\begin{align} *) \, x_0 = x_p & = \frac{-b}{2a} = \frac{-(-3)}{2.\frac{1}{5}} = \frac{15}{2} \\ *) \, y_0 = y_p & = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} \\ & = \frac{(-3)^2 - 4. \frac{1}{5}. 10 }{-4.\frac{4}{5}} \\ & = \frac{9-8}{-\frac{4}{5}} = - \frac{5}{4} \end{align}$
Sehingga nilai :

$x_0 + y_0 = \frac{15}{2} + (-\frac{5}{4}) = \frac{25}{4}$
Jadi, nilai

$x_0 + y_0 = \frac{25}{4} . \heartsuit$

Nomor 7

Pada segitiga siku-siku ABC dengan

$AC \bot BC \,$ dan panjang

$AC \,$ adalah

$\frac{5}{2} BC \,$ .
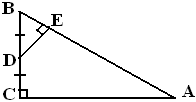
spmk_ub_1_2010

Jika D titik tengah BC dan

$DE \bot AB \,$ , maka perbandingan luas daerah

$\Delta ABC : \Delta DBE \,$ adalah ....

$\clubsuit \,$ Gambar
spmk_ub_1a_2010

Misal panjang

$BD = x , \,$ panjang yang lainnya :

$CD = x, \, BC = 2x$

$AC = \frac{5}{2}BC = \frac{5}{2}.2x = 5x$

$AB = \sqrt{AC^2 + BC^2 } = \sqrt{(5x)^2 + (2x)^2}$

$AB = \sqrt{29x^2}=x\sqrt{29}$

$\clubsuit \,$ Menentukan panjang BE dan ED dengan konsep kesebangunan

$\Delta BED \,$ sebangun dengan

$\Delta ABC \,$ pada gambar 2 dan gambar 3

$\frac{BE}{BC}=\frac{BD}{BA} \rightarrow \frac{BE}{2x}=\frac{x}{x\sqrt{29}} \rightarrow BE = \frac{2x}{\sqrt{29}}$

$\frac{ED}{AC}=\frac{BD}{BA} \rightarrow \frac{ED}{5x}=\frac{x}{x\sqrt{29}} \rightarrow ED = \frac{5x}{\sqrt{29}}$

$\clubsuit \,$ Menentukan perbandingan luasnya

$\begin{align} \frac{L \, \Delta ABC }{L \, \Delta DBE } & = \frac{\frac{1}{2}. AC.BC}{\frac{1}{2}.ED.BE} \\ & = \frac{\frac{1}{2}. 5x.2x}{\frac{1}{2}.\frac{5x}{\sqrt{29}}.\frac{2x}{\sqrt{29}}} \\ & = 5x.2x. \frac{\sqrt{29}}{5x} . \frac{\sqrt{29}}{2x} \\ & = \frac{29}{1} \end{align}$
Jadi, perbandingan luasnya adalah 29 : 1 .

$\heartsuit$

Nomor 8

Jika pertidaksamaan

$3x -p > \frac{x-2}{3} + px \,$ mempunyai penyelesaian

$x > 5 , \,$ maka nilai

$p \,$ adalah ....

$\spadesuit \,$ Kelompokkan pertidaksamaan

$\begin{align} 3x -p & > \frac{x-2}{3} + px \, \, \, \, \text{(kali 3)} \\ 9x - 3p & > x-2 + 3px \\ 9x - x - 3px & > 3p - 2 \\ (8-3p)x & > 3p - 2 \\ x & > \frac{3p-2}{8-3p} \, \, \, \, \text{...pert(i)} \end{align}$
Solusi pertidaksamaan

$x > 5 \,$ , artinya bentuk

$x > \frac{3p-2}{8-3p} \,$ sama dengan

$x > 5 \,$ , sehingga diperoleh

$\frac{3p-2}{8-3p} = 5$

$\spadesuit \,$ Menentukan nilai

$p$

$\begin{align} \frac{3p-2}{8-3p} & = 5 \\ 3p-2 & = 5(8-3p) \\ 3p-2 & = 40 - 15p \\ 18p & = 42 \\ p & = \frac{42}{18} = \frac{7}{3} \end{align}$
Jadi, nilai

$p = \frac{7}{3} . \heartsuit$
Catatan : tidak ada pada pilihan.

Cara II :

$\spadesuit \,$ Solusi pertidaksamaan

$x > 5 , \,$ artinya

$x = 5\,$ adalah akar dari pertidaksamaannya. Substitusi

$x= 5 \,$ ke pertidaksamaanya dan tanda ketaksamaanya

$( > , \, \geq , \, \leq , \, < ) \,$ menjadi sama dengan.

$\begin{align} x=5 \rightarrow 3x -p & > \frac{x-2}{3} + px \\ 3.5 -p & = \frac{5-2}{3} + p.5 \\ 15 -p & = \frac{3}{3} + 5p \\ 15 -p & = 1 + 5p \\ 6p & = 14 \\ p & = \frac{14}{6} = \frac{7}{3} \end{align}$
Jadi, nilai

$p = \frac{7}{3} . \heartsuit$
Catatan : tidak ada pada pilihan.

Nomor 9

Perhatikan gambar

$\Delta PQR \,$ dengan

$\angle Q = 30^\circ , \,$ RS adalah garis tinggi dari titik sudut R. Jika

$QR = a \,$ dan

$PR = \frac{1}{2}\sqrt{3}a , \,$ maka rasio

$PR \,$ terhadap

$SQ \,$ adalah ....

$\clubsuit \,$ gambar
spmk_ub_3_2010

$\clubsuit \,$ Menentukan panjang SQ pada segitiga QRS

$\begin{align} \cos 30^\circ & = \frac{SQ}{QR} \\ \frac{1}{2}\sqrt{3} & = \frac{SQ}{a} \\ SQ & = \frac{1}{2}\sqrt{3}a \end{align}$

$\clubsuit \,$ Menentukan rasio (perbandingan)

$\begin{align} \frac{PR}{SQ} & = \frac{\frac{1}{2}\sqrt{3}a}{\frac{1}{2}\sqrt{3}a} = 1 \end{align}$
Jadi, rasio PR terhadap SQ adalah 1.

$\heartsuit$

Nomor 10

Sebuah cakram yang terbuat dari logam mengalami pemuaian sehingga jari-jarinya bertambah 20% dari jari-jari semula. Berapa persen pertambahan luas cakram tersebut dengan adanya pemuaian ?

$\spadesuit \,$ Permisalan

$L_a \,$ = luas awal cakram =

$\pi r^2$

$r \,$ = jari-jari awal cakram

$L_p \,$ = Luas adanya pemuaian =

$\pi (r_p)^2$

$r_p \,$ = jari-jari adanya pemuaian

$\spadesuit \,$ Jari-jari bertambah 20%

$\begin{align} r_p & = r + 20\% r = r + 0,2r = 1,2r \end{align}$

$\spadesuit \,$ Luas adanya pemuaian

$\begin{align} L_p & = \pi (r_p)^2 \\ & = \pi (1,2r)^2 \\ & = 1,44\pi r^2 \\ & = \pi r^2 + 0,44 \pi r^2 \\ & = \pi r^2 + 0,44 \times 100\% \pi r^2 \\ & = \pi r^2 + 44 \% \pi r^2 \end{align}$
Artinya Luas adanya pemuaian bertambah 44% dari luas awalnya sebelum adanya pemuaian.
Jadi, luasnya bertambah 44% .

$\heartsuit$

Nomor Soal Lainnya : 1-5 6-10 11-15

Tidak ada komentar:

Posting Komentar

Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.

dunia informa

Pages - Menu