Nomor 11
Persamaan garis singgung lingkaran dengan L:x2+y2−6x+8y=0 yang tegak lurus pada garis x+y=1 adalah ....
♣ Konsep dasar lingkaran
*) Unsur-unsur lingkaran :
Persamaan lingkaran : x2+y2+Ax+By+C=0
Pusat (a,b) : a−A2,b=−B2
Jari-jari : r=√a2+b2−C
*) Persamaan garis singgung (PGS) lingkaran
PGQ nya : y−b=m(x−a)±r√1+m2
♣ Menentukan unsur-unsur lingkaran
x2+y2−6x+8y=0→A=−6,B=8,C=0
pusat (a,b) dan jari-jari
a=−A2=−(−6)2=3,b=−B2=−82=−4
r=√a2+b2−C=√32+(−4)2−0=√25=5
♣ Menentukan gradien garis singgungnya
x+y=1→y=−x+1→m1=−1
garis singgung tegak lurus dengan garis x+y=1 sehingga
m.m1=−1→m.(−1)=−1→m=1
artinya gradien garis singgungnya m=1
♣ Menentukan PGS nya dengan a=3,b=−4,r=5,m=1
y−b=m(x−a)±r√1+m2y−(−4)=1.(x−3)±5√1+12y+4=(x−3)±5√2y=x−7±5√2
Jadi, PGS nya adalah y=x−7±5√2.♡
*) Unsur-unsur lingkaran :
Persamaan lingkaran : x2+y2+Ax+By+C=0
Pusat (a,b) : a−A2,b=−B2
Jari-jari : r=√a2+b2−C
*) Persamaan garis singgung (PGS) lingkaran
PGQ nya : y−b=m(x−a)±r√1+m2
♣ Menentukan unsur-unsur lingkaran
x2+y2−6x+8y=0→A=−6,B=8,C=0
pusat (a,b) dan jari-jari
a=−A2=−(−6)2=3,b=−B2=−82=−4
r=√a2+b2−C=√32+(−4)2−0=√25=5
♣ Menentukan gradien garis singgungnya
x+y=1→y=−x+1→m1=−1
garis singgung tegak lurus dengan garis x+y=1 sehingga
m.m1=−1→m.(−1)=−1→m=1
artinya gradien garis singgungnya m=1
♣ Menentukan PGS nya dengan a=3,b=−4,r=5,m=1
y−b=m(x−a)±r√1+m2y−(−4)=1.(x−3)±5√1+12y+4=(x−3)±5√2y=x−7±5√2
Jadi, PGS nya adalah y=x−7±5√2.♡
Nomor 12
Diketahui suku banyak g(x)=x3+x2−x+b habis dibagi (x−1) . Jika g(x) dibagi (x2−1) ,
maka sisanya adalah .....
♠ Teorema sisa : f(x)x−a⇒sisa=f(a)
artinya : substitusi x=a ke f(x) dengan hasil sama dengan sisanya
♠ Menentukan nilai b pada g(x)=x3+x2−x+b
g(x):(x−1)→ sisa = g(1)
Karena habis dibagi, maka sisanya sama dengan nol.
sisa =g(1)0=g(1)0=13+12−1+bb=−1
Fungsinya menjadi : g(x)=x3+x2−x−1
♠ Menentukan sisa g(x) dibagi (x2−1)
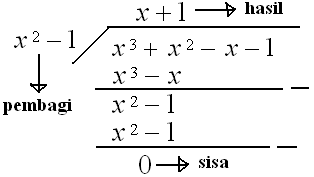
sehingga sisanya = 0
Jadi, sisa g(x) dibagi (x2−1) adalah 0 . ♡
artinya : substitusi x=a ke f(x) dengan hasil sama dengan sisanya
♠ Menentukan nilai b pada g(x)=x3+x2−x+b
g(x):(x−1)→ sisa = g(1)
Karena habis dibagi, maka sisanya sama dengan nol.
sisa =g(1)0=g(1)0=13+12−1+bb=−1
Fungsinya menjadi : g(x)=x3+x2−x−1
♠ Menentukan sisa g(x) dibagi (x2−1)

sehingga sisanya = 0
Jadi, sisa g(x) dibagi (x2−1) adalah 0 . ♡
Nomor 13
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Misalkan P adalah titik potong diagonal ABCD dan Q adalah
proyeksi B pada PF. Panjang PQ adalah ......
♣ Gambar
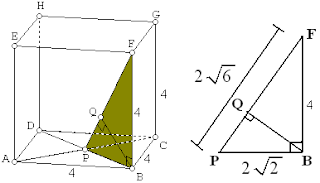
Proyeksi B pada PF adalah titik Q dengan syarat garis BQ tegak lurus dengan PF.
♣ Menentukan panjang sisi lainnya
PB=12BD=12.4√2=2√2
ΔPBF→PF=√PB2+BF2=√(2√2)2+42=2√6
♣ Menentukan panjang BQ dengan luas ΔPBF
LΔPBF (alas PF)=LΔPBF (alas PB)12.PF.BQ=12.PB.BF12.2√6.BQ=12.2√2.4BQ=4√2√6=43√3
♣ Menentukan panjang PQ pada segitiga PBQ
PQ=√PB2−BQ2=√(2√2)2−(43√3)2=√8−163=√83=2√2√3PQ=23√6
Jadi, panjang PQ=23√6.♡

Proyeksi B pada PF adalah titik Q dengan syarat garis BQ tegak lurus dengan PF.
♣ Menentukan panjang sisi lainnya
PB=12BD=12.4√2=2√2
ΔPBF→PF=√PB2+BF2=√(2√2)2+42=2√6
♣ Menentukan panjang BQ dengan luas ΔPBF
LΔPBF (alas PF)=LΔPBF (alas PB)12.PF.BQ=12.PB.BF12.2√6.BQ=12.2√2.4BQ=4√2√6=43√3
♣ Menentukan panjang PQ pada segitiga PBQ
PQ=√PB2−BQ2=√(2√2)2−(43√3)2=√8−163=√83=2√2√3PQ=23√6
Jadi, panjang PQ=23√6.♡
Nomor 14
Petunjuk C digunakan untuk nomor 14 dan 15 .
Diketahui garis g adalah garis singgung kurva x2y=32 di titik (2,8). Pernyataan berikut yang benar adalah ....
(1). Garis g memotong sumbu X di titik (6,0)
(2). Garis g memotong sumbu Y di titik (0,18)
(3). Luas daerah dibawah garis g pada kuadran pertama adalah 36
(4). Persamaan garis g adalah y=−3x+18
Diketahui garis g adalah garis singgung kurva x2y=32 di titik (2,8). Pernyataan berikut yang benar adalah ....
(1). Garis g memotong sumbu X di titik (6,0)
(2). Garis g memotong sumbu Y di titik (0,18)
(3). Luas daerah dibawah garis g pada kuadran pertama adalah 36
(4). Persamaan garis g adalah y=−3x+18
♠ Persamaan garis singgung (PGS) di titik (x1,y1), adalah
y−y1=m(x−x1) dengan gradien m=f′(x1)
♠ Menentukan gradien garis singgungnya di titik (2,8), artinya gradien m=f′(2)
konsep turunan : y=axn→y′=n.a.xn−1
x2y=32y=32x2=32x−2y′=−2.32.x−3=−64x3m=f′(2)=−6423=−8
♠ Menentukana PGS nya di (x1,y1)=(2,8) dan m=−8
y−y1=m(x−x1)y−8=−8(x−2)y−8=−8x+16y=−8x+24
Sehingga PGS nya : y=−8x+24
♠ Cek pernyataan (1) sampai (4)
(1). titik potong sumbu X , substitusi y=0
y=−8x+24→0=−8x+24→x=3
sehingga titik potongnya (3,0) . (pernyataan (1) salah)
(2). titik potong sumbu Y , substitusi x=0
y=−8x+24→y=−8.0+24→y=24
sehingga titik potongnya (0,24) . (pernyataan (2) salah)
(3). gambar

Luas arsir = 12.a.t=12.3.24=36
pernyataan (3) benar.
(4). Pernyataan (4) salah karena PGSnya : y=−8x+24
Jadi, yang benar hanya pernyataan (3), tidak ada pilihannya. ♡
♠ Menentukan gradien garis singgungnya di titik (2,8), artinya gradien m=f′(2)
konsep turunan : y=axn→y′=n.a.xn−1
x2y=32y=32x2=32x−2y′=−2.32.x−3=−64x3m=f′(2)=−6423=−8
♠ Menentukana PGS nya di (x1,y1)=(2,8) dan m=−8
y−y1=m(x−x1)y−8=−8(x−2)y−8=−8x+16y=−8x+24
Sehingga PGS nya : y=−8x+24
♠ Cek pernyataan (1) sampai (4)
(1). titik potong sumbu X , substitusi y=0
y=−8x+24→0=−8x+24→x=3
sehingga titik potongnya (3,0) . (pernyataan (1) salah)
(2). titik potong sumbu Y , substitusi x=0
y=−8x+24→y=−8.0+24→y=24
sehingga titik potongnya (0,24) . (pernyataan (2) salah)
(3). gambar

Luas arsir = 12.a.t=12.3.24=36
pernyataan (3) benar.
(4). Pernyataan (4) salah karena PGSnya : y=−8x+24
Jadi, yang benar hanya pernyataan (3), tidak ada pilihannya. ♡
Nomor 15
Untuk dua himpunan A dan B , didefinisikan
A−B={x|x∈Adanx∉B} dan
A+B=(A∪B)−(A∩B) .
Syarat yang harus dipenuhi agar A+B memiliki anggota himpunan yang sama dengan A−B adalah ...
(1). A∩B=∅
(2). B=∅
(3). A≠B
(4). B⊆A
A−B={x|x∈Adanx∉B} dan
A+B=(A∪B)−(A∩B) .
Syarat yang harus dipenuhi agar A+B memiliki anggota himpunan yang sama dengan A−B adalah ...
(1). A∩B=∅
(2). B=∅
(3). A≠B
(4). B⊆A
♣ Konsep dasar himpunan
∅= himpunan kosong (tidak ada anggotanya)
S= himpunan semesta (ruang sampel)
(∅)c=S artinya komplemen (lawan) dari himpunan kosong adalah himpunan semesta
x∈A artinya x anggota dari himpunan A
x∉A artinya x bukan anggota dari himpunan A
x∉A sama saja dengan x∈Ac
∪= gabungan dua himpunan (diambil semua)
∩= irisan dua himpunan (diambil yang sama)
A∪∅=A,A∩∅=∅
A∪S=S,A∩S=A
♣ Menyederhanakan definisinya
*) definisi pertama :
A−B={x|x∈Adanx∉B}A−B={x|x∈Adanx∈Bc}A−B={x|x∈(A∩Bc)}A−B=(A∩Bc)...(i)
*) definisi kedua menggunakan bentuk (i)
A+B=(A∪B)−(A∩B)A+B=(A∪B)∩(A∩B)c...(ii)
♣ Cek semua pernyataan menggunakan bentuk (i) dan (ii)
(1). A∩B=∅
cek bentuk (ii) :
A+B=(A∪B)∩(A∩B)cA+B=(A∪B)∩(∅)cA+B=(A∪B)∩SA+B=(A∪B)
dari A+B=(A∪B) dan A−B=(A∩Bc) maka hasilnya tidak sama, yang artinya A+B≠A−B. pernyataan (1) salah.
(2). B=∅
cek kedua bentuk (i) dan (ii) :
bentuk (i) : A+B=(A∪B)∩(A∩B)cA+B=(A∪∅)∩(A∩∅)cA+B=(A)∩(∅)cA+B=(A)∩SA+B=(A)bentuk (ii) : A−B=(A∩Bc)A−B=(A∩(∅)c)A−B=(A∩S)A−B=A
karena diperoleh A+B=A dan A−B=A , maka hasilnya sama, artinya A+B=A−B sehingga pernyataan (2) benar.
(3). A≠B
karena A≠B , maka bisa saja hasilnya A∩B=∅ , sehingga dari pernyataan (1) maka pernyataan (3) juga salah.
(4). B⊆A
B⊆A artinya semua anggota B ada di dalam himpunan A atau bisa saja A=B
cek kedua bentuk (i) dan (ii) :
bentuk (i) : A+B=(A∪B)∩(A∩B)cA+B=(A)∩(B)c=(A∩Bc)
karena diperoleh A+B=(A∩Bc) dan A−B=(A∩Bc) , maka hasilnya sama, artinya A+B=A−B sehingga pernyataan (4) benar.
Jadi, pernyataan yang benar adalah (2) dan (4), sehingga pilihannya C. ♡
∅= himpunan kosong (tidak ada anggotanya)
S= himpunan semesta (ruang sampel)
(∅)c=S artinya komplemen (lawan) dari himpunan kosong adalah himpunan semesta
x∈A artinya x anggota dari himpunan A
x∉A artinya x bukan anggota dari himpunan A
x∉A sama saja dengan x∈Ac
∪= gabungan dua himpunan (diambil semua)
∩= irisan dua himpunan (diambil yang sama)
A∪∅=A,A∩∅=∅
A∪S=S,A∩S=A
♣ Menyederhanakan definisinya
*) definisi pertama :
A−B={x|x∈Adanx∉B}A−B={x|x∈Adanx∈Bc}A−B={x|x∈(A∩Bc)}A−B=(A∩Bc)...(i)
*) definisi kedua menggunakan bentuk (i)
A+B=(A∪B)−(A∩B)A+B=(A∪B)∩(A∩B)c...(ii)
♣ Cek semua pernyataan menggunakan bentuk (i) dan (ii)
(1). A∩B=∅
cek bentuk (ii) :
A+B=(A∪B)∩(A∩B)cA+B=(A∪B)∩(∅)cA+B=(A∪B)∩SA+B=(A∪B)
dari A+B=(A∪B) dan A−B=(A∩Bc) maka hasilnya tidak sama, yang artinya A+B≠A−B. pernyataan (1) salah.
(2). B=∅
cek kedua bentuk (i) dan (ii) :
bentuk (i) : A+B=(A∪B)∩(A∩B)cA+B=(A∪∅)∩(A∩∅)cA+B=(A)∩(∅)cA+B=(A)∩SA+B=(A)bentuk (ii) : A−B=(A∩Bc)A−B=(A∩(∅)c)A−B=(A∩S)A−B=A
karena diperoleh A+B=A dan A−B=A , maka hasilnya sama, artinya A+B=A−B sehingga pernyataan (2) benar.
(3). A≠B
karena A≠B , maka bisa saja hasilnya A∩B=∅ , sehingga dari pernyataan (1) maka pernyataan (3) juga salah.
(4). B⊆A
B⊆A artinya semua anggota B ada di dalam himpunan A atau bisa saja A=B
cek kedua bentuk (i) dan (ii) :
bentuk (i) : A+B=(A∪B)∩(A∩B)cA+B=(A)∩(B)c=(A∩Bc)
karena diperoleh A+B=(A∩Bc) dan A−B=(A∩Bc) , maka hasilnya sama, artinya A+B=A−B sehingga pernyataan (4) benar.
Jadi, pernyataan yang benar adalah (2) dan (4), sehingga pilihannya C. ♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.