Nomor 6
Diketahui bahwa persamaan kuadrat x2+ax+b=0 mempunyai akar-akar real x1>0 dan x2>0 .
Jika x1,x2,x21x2 , membentuk deret geometri dengan rasio 4, maka ab adalah ....
♠ PK : x2+ax+b=0 akar-akarnya x1 dan x2
*) x1+x2=−ba=−a1=−a
artinya : x1+x2=−a→a=−(x1+x2)
*) x1.x2=ca=b1=b
artinya : x1.x2=b→b=x1.x2
♠ Barisan geometri : x1,x2,x21x2
Rasionya (r) sama dengan 4 :
r=x2x1=x21x2x2=4∗)x21x2x2=4→x21=4→x1=2∗)x2x1=4→x2=4x1=4.2=8
♠ Menentukan nilai ab
ab=−(x1+x2)x1.x2=−(2+8)2.8=−1016ab=−58
Jadi, nilai ab=−58.♡
*) x1+x2=−ba=−a1=−a
artinya : x1+x2=−a→a=−(x1+x2)
*) x1.x2=ca=b1=b
artinya : x1.x2=b→b=x1.x2
♠ Barisan geometri : x1,x2,x21x2
Rasionya (r) sama dengan 4 :
r=x2x1=x21x2x2=4∗)x21x2x2=4→x21=4→x1=2∗)x2x1=4→x2=4x1=4.2=8
♠ Menentukan nilai ab
ab=−(x1+x2)x1.x2=−(2+8)2.8=−1016ab=−58
Jadi, nilai ab=−58.♡
Nomor 7
Nilai lim adalah ....
\clubsuit \, Konsep dasar limit
\displaystyle \lim_{x \to \infty } \sqrt{ax^2+bx+c}-\sqrt{ax^2+px+q} = \frac{b-p}{2\sqrt{a}}
\clubsuit \, Menentukan hasil limitnya dengan modifikasi
\begin{align} \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{2}x & = \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{(\sqrt{2}x)^2} \\ & = \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{2x^2} \\ & b = 0 , \, p = 0 , \, a = 2 \\ & = \frac{b-p}{2\sqrt{a}} = \frac{0-0}{2\sqrt{2}} = 0 \end{align}
Jadi, nilai limitnya adalah 0 . \heartsuit
\displaystyle \lim_{x \to \infty } \sqrt{ax^2+bx+c}-\sqrt{ax^2+px+q} = \frac{b-p}{2\sqrt{a}}
\clubsuit \, Menentukan hasil limitnya dengan modifikasi
\begin{align} \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{2}x & = \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{(\sqrt{2}x)^2} \\ & = \displaystyle \lim_{x \to \infty } \sqrt{2x^2-9} - \sqrt{2x^2} \\ & b = 0 , \, p = 0 , \, a = 2 \\ & = \frac{b-p}{2\sqrt{a}} = \frac{0-0}{2\sqrt{2}} = 0 \end{align}
Jadi, nilai limitnya adalah 0 . \heartsuit
Nomor 8
Nilai maksimum f(x,y) = 8x+5y \, untuk x \, dan y \, di daerah yang diarsir adalah ....


\spadesuit \, Konsep persamaan garis
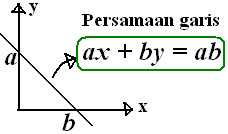
\spadesuit \, Menentukan persamaan garisnya

garis I : 9x + 3y = 9.3 \rightarrow 3x+y = 9
garis II : 6x+4y=6.4 \rightarrow 3x+2y=12
\spadesuit \, Eliminasi kedua persamaan untuk menentukan titik B
\begin{array}{cc} 3x+2y=12 & \\ 3x+y = 9 & - \\ \hline y = 3 & \end{array}
pers(i) : 3x+y = 9 \rightarrow 3x+3 = 9 \rightarrow x = 2
sehingga titik B(2,3)
\spadesuit \, Menentukan nilai maksimum f(x,y) = 8x+5y \, dengan substitusi semua titik pojoknya
\begin{align} A(3,0) \rightarrow f & = 8.3+5.0 = 24 \\ B(2,3) \rightarrow f & = 8.2+5.3 = 16+15=31 \\ C(0,6) \rightarrow f & = 8.0+5.6 = 30 \end{align}
Jadi, nilai maksimumnya adalah 31. \heartsuit

\spadesuit \, Menentukan persamaan garisnya

garis I : 9x + 3y = 9.3 \rightarrow 3x+y = 9
garis II : 6x+4y=6.4 \rightarrow 3x+2y=12
\spadesuit \, Eliminasi kedua persamaan untuk menentukan titik B
\begin{array}{cc} 3x+2y=12 & \\ 3x+y = 9 & - \\ \hline y = 3 & \end{array}
pers(i) : 3x+y = 9 \rightarrow 3x+3 = 9 \rightarrow x = 2
sehingga titik B(2,3)
\spadesuit \, Menentukan nilai maksimum f(x,y) = 8x+5y \, dengan substitusi semua titik pojoknya
\begin{align} A(3,0) \rightarrow f & = 8.3+5.0 = 24 \\ B(2,3) \rightarrow f & = 8.2+5.3 = 16+15=31 \\ C(0,6) \rightarrow f & = 8.0+5.6 = 30 \end{align}
Jadi, nilai maksimumnya adalah 31. \heartsuit
Nomor 9
Nilai x \, yang memenuhi persamaan \left( 8^{x + \frac{1}{3}} \right)^2 = 0,5\sqrt[3]{2^x} \, adalah ....
\clubsuit \, Konsep eksponen
*) sifat eksponen
(a^m)^n = a^{m.n}, \, \, \, \, a^m.a^n = a^{m+n}
(a)^{-n} = \frac{1}{a^n}, \, \, \, \, \sqrt[n]{a^m} = a^\frac{m}{n}
*) Persamaan : a^{f(x)} = a^{g(x)} \rightarrow f(x) = g(x)
\clubsuit \, Menentukan nilai x
\begin{align} \left( 8^{x + \frac{1}{3}} \right)^2 & = 0,5\sqrt[3]{2^x} \\ 8^{2x + \frac{2}{3}} & = \frac{1}{2}.2^\frac{x}{3} \\ (2^3)^{2x + \frac{2}{3}} & = 2^{-1}.2^\frac{x}{3} \\ 2^{6x + 2} & = 2^{-1 + \frac{x}{3}} \\ 6x + 2 & = -1 + \frac{x}{3} \, \, \, \, \text{(kali 3)} \\ 18x + 6 & = -3 + x \\ 17x & = -9 \\ x & = \frac{-9}{17} \end{align}
Jadi, nilai x = \frac{-9}{17} . \heartsuit
*) sifat eksponen
(a^m)^n = a^{m.n}, \, \, \, \, a^m.a^n = a^{m+n}
(a)^{-n} = \frac{1}{a^n}, \, \, \, \, \sqrt[n]{a^m} = a^\frac{m}{n}
*) Persamaan : a^{f(x)} = a^{g(x)} \rightarrow f(x) = g(x)
\clubsuit \, Menentukan nilai x
\begin{align} \left( 8^{x + \frac{1}{3}} \right)^2 & = 0,5\sqrt[3]{2^x} \\ 8^{2x + \frac{2}{3}} & = \frac{1}{2}.2^\frac{x}{3} \\ (2^3)^{2x + \frac{2}{3}} & = 2^{-1}.2^\frac{x}{3} \\ 2^{6x + 2} & = 2^{-1 + \frac{x}{3}} \\ 6x + 2 & = -1 + \frac{x}{3} \, \, \, \, \text{(kali 3)} \\ 18x + 6 & = -3 + x \\ 17x & = -9 \\ x & = \frac{-9}{17} \end{align}
Jadi, nilai x = \frac{-9}{17} . \heartsuit
Nomor 10
Petunjuk B digunakan untuk menjawab soal nomor 10 dan 11.
Grafik y=px^2 +qx+4 \, melalui titik (x,y)=(0,4) \, untuk semua nilai p \, dan q \, . Jika grafik tersebut juga melewati (1,3) dan (2,6) , maka nilai 3p+q=3 \, .
SEBAB
p =3 \, dan q = -6 .
Grafik y=px^2 +qx+4 \, melalui titik (x,y)=(0,4) \, untuk semua nilai p \, dan q \, . Jika grafik tersebut juga melewati (1,3) dan (2,6) , maka nilai 3p+q=3 \, .
SEBAB
p =3 \, dan q = -6 .
\spadesuit \, Substitusi titik (1,3) dan (2,6) ke y=px^2 +qx+4
\begin{align} (x,y)=(1,3) \rightarrow y & =px^2 +qx+4 \\ 3 & =p.1^2 +q.1+4 \\ p+q & = -1 \, \, \, \, \text{...pers(i)} \\ (x,y)=(2,6) \rightarrow y & =px^2 +qx+4 \\ 6 & =p.2^2 +q.2+4 \\ 4p+2q & = 2 \, \, \, \, \text{(bagi 2)} \\ 2p+q & = 1 \, \, \, \, \text{...pers(ii)} \end{align}
\spadesuit \, Eliminasi pers(i) dan pers(ii)
\begin{array}{cc} 2p+q = 1 & \\ p+q = -1 & - \\ \hline p = 2 & \end{array}
pers(i) : p+q = -1 \rightarrow 2+q = -1 \rightarrow q = -3
sehingga nilai 3p+q = 3.2 + (-3) = 3
\spadesuit \, Berdasarkan petunjuk B
*) Pernyataan pertama : 3p + q = 3 \, (benar)
*) Pernyataan kedua : p = 3 \, dan q = -6 \, salah karena seharusnya nilai p = 2 \, dan q = -3
Karena pernyataan pertama benar dan pernyataan kedua salah, maka berdasarkan petunjuk B jawabannya opsi C.
Jadi, jawabannya C. \heartsuit
\begin{align} (x,y)=(1,3) \rightarrow y & =px^2 +qx+4 \\ 3 & =p.1^2 +q.1+4 \\ p+q & = -1 \, \, \, \, \text{...pers(i)} \\ (x,y)=(2,6) \rightarrow y & =px^2 +qx+4 \\ 6 & =p.2^2 +q.2+4 \\ 4p+2q & = 2 \, \, \, \, \text{(bagi 2)} \\ 2p+q & = 1 \, \, \, \, \text{...pers(ii)} \end{align}
\spadesuit \, Eliminasi pers(i) dan pers(ii)
\begin{array}{cc} 2p+q = 1 & \\ p+q = -1 & - \\ \hline p = 2 & \end{array}
pers(i) : p+q = -1 \rightarrow 2+q = -1 \rightarrow q = -3
sehingga nilai 3p+q = 3.2 + (-3) = 3
\spadesuit \, Berdasarkan petunjuk B
*) Pernyataan pertama : 3p + q = 3 \, (benar)
*) Pernyataan kedua : p = 3 \, dan q = -6 \, salah karena seharusnya nilai p = 2 \, dan q = -3
Karena pernyataan pertama benar dan pernyataan kedua salah, maka berdasarkan petunjuk B jawabannya opsi C.
Jadi, jawabannya C. \heartsuit
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.