Pembahasan Soal SPMK UB Matematika IPA Kode 81 tahun 2008 nomor 6 sampai 10

Nomor 6

Luas daerah yang dibatasi oleh garis

$y = x-1 \,$ dan parabola

$y^2 = 2x + 6 \,$ adalah .... satuan.

$\spadesuit \,$ gambar

$y = x-1 \rightarrow x = y+1$

$y^2 = 2x + 6 \rightarrow x = \frac{1}{2}y^2 - 3$
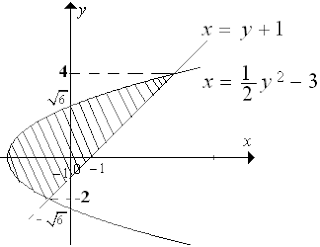
spmk_ub_2_2008

Titik potong kedua kurva :

$\begin{align} x_1 & = x_2 \\ \frac{1}{2}y^2 - 3 & = y + 1 \, \, \, \, \text{(kalii 2)} \\ y^2 -6 & = 2y + 2 \\ y^2 - 2y -8 & = 0 \\ (y-4)(y+2) & = 0 \\ y=4 \vee y & = -2 \end{align}$

$\spadesuit \,$ Menentukan luas daerah arsiran

$\begin{align} L & = \int \limits_{-2}^4 \text{ (kurva kanan)} - \text{ (kurva kiri)} dy \\ L & = \int \limits_{-2}^4 (y+1) - (\frac{1}{2}y^2 - 3) dy \\ L & = \int \limits_{-2}^4 ( -\frac{1}{2}y^2 + y + 4 ) \, dy \\ L & = ( -\frac{1}{6}y^3 + \frac{1}{2}y^2 + 4y )|_{-2}^4 \\ L & = ( -\frac{1}{6}.4^3 + \frac{1}{2}.4^2 + 4.4 ) - \\ & ( -\frac{1}{6}.(-2)^3 + \frac{1}{2}.(-2)^2 + 4.(-2) ) \\ L & = ( -\frac{32}{3} + 8 + 16 ) - ( \frac{4}{3} + 2 + -8 ) \\ L & = 18 \end{align}$
Jadi, luas daerahnya adalah 18.

$\heartsuit$

Cara II :

$\spadesuit \,$ Luas daerah tertutup yang dibatasi oleh dua kurva (garis dengan parabola atau parabola dengan parabola) adalah

$L = \frac{D\sqrt{D}}{6a^2} \,$ dengan

$D = b^2-4ac$

$\spadesuit \,$ Substitusi garis ke parabola

$\begin{align} y & = x - 1 \rightarrow x = y+1 \\ y^2 & = 2x + 6 \rightarrow x = \frac{1}{2} y^2 - 3 \\ \frac{1}{2} y^2 - 3 & = y+1 \\ \frac{1}{2} y^2 -y -4 & = 0 \rightarrow a = \frac{1}{2}, \, b = -1, \, c = -4 \\ D & = b^2 - 4ac \\ D & = (-1)^2 - 4.(\frac{1}{2}).(-4) = 1 + 8 = 9 \\ L & = \frac{D\sqrt{D}}{6a^2} = \frac{9\sqrt{9}}{6.(\frac{1}{2})^2} = 18 \end{align}$
Jadi, luas daerahnya adalah 18.

$\heartsuit$

Nomor 7

$\displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} = .....$

Cara I : Menggunakan turunan

$\clubsuit \,$ Penerapan turunan pada limit

$\displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \,$ solusinya

$\displaystyle \lim_{x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to k } \frac{f^\prime (x)}{g^\prime (x)} \,$ diturunkan sampai hasilnya tidak

$\frac{0}{0}$
Turunan akar :

$y = \sqrt{f(x)} \rightarrow y^\prime = \frac{f^\prime (x)}{2\sqrt{f(x)}}$

$\clubsuit \,$ Menentukan hasil limitnya

$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\frac{1}{2\sqrt{x}} - 1}{1-2x} \\ & = \frac{\frac{1}{2\sqrt{1}} - 1}{1-2.1} \\ & = \frac{\frac{1}{2} - 1}{1-2} = \frac{-\frac{1}{2}}{-1} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah

$\frac{1}{2} . \heartsuit$

Cara II : Merasionalkan bentuk akar

$\clubsuit \,$ Konsep kali sekawan

$(\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q}) = (\sqrt{p})^2-(\sqrt{q})^2 = p-q$

$\clubsuit \,$ Menentukan hasil limitnya

$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} . \frac{\sqrt{x} + x}{\sqrt{x} + x} \\ & = \displaystyle \lim_{x \to 1 } \frac{(x-x^2)}{(x-x^2)(\sqrt{x} + x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{1}{(\sqrt{x} + x)} \\ & = \frac{1}{(\sqrt{1} + 1)} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah

$\frac{1}{2} . \heartsuit$

Cara III : Pemfaktoran

$\clubsuit \,$ Konsep pemfaktoran :

$p-q = (\sqrt{p}-\sqrt{q})(\sqrt{p}+\sqrt{q})$

$\clubsuit \,$ Menentukan hasil limitnya

$\begin{align} \displaystyle \lim_{x \to 1 } \frac{\sqrt{x} - x}{x-x^2} & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-x)} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}(1-\sqrt{x})}{x(1-\sqrt{x})(1+\sqrt{x})} \\ & = \displaystyle \lim_{x \to 1 } \frac{\sqrt{x}}{x(1+\sqrt{x})} \\ & = \frac{\sqrt{1}}{1.(1+\sqrt{1})} \\ & = \frac{1}{2} \end{align}$
Jadi, nilai limitnya adalah

$\frac{1}{2} . \heartsuit$

Nomor 8

Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jika nilai terkecil dan terbesar dari fungsi

$f(x) = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \,$ adalah

$a \,$ dan

$b \,$ ,
maka nilai

$a + b = 6$
SEBAB

$a = -5 \,$ dan

$b = 11 .$

$\spadesuit \,$ Konsep dasar trigonometri
*)

$\cos A \cos B = \frac{1}{2} [\cos (A+B) + \cos (A-B) ]$
*) Nilai maksimum/minimum dari :

$f(x) = P\cos g(x) + c \,$

$f_\text{maks} = |P| + c \,$ dan

$f_\text{min} = -|P| + c$

$\spadesuit \,$ Menyederhanakan soalnya
Misal :

$A = \left( x - \frac{\pi}{4} \right) \,$ dan

$B = \left( x + \frac{\pi}{4} \right)$

$A + B = \left( x - \frac{\pi}{4} \right) + \left( x + \frac{\pi}{4} \right) = 2x$

$A - B = \left( x - \frac{\pi}{4} \right) - \left( x + \frac{\pi}{4} \right) = \frac{-\pi}{2}$
Substitusi nilai

$A \,$ dan

$B \,$ pada fungsinya :

$\begin{align} f(x) & = 8 \cos \left( x - \frac{\pi}{4} \right) \cos \left( x + \frac{\pi}{4} \right) + 3 \\ f(x) & = 8 \cos A \cos B + 3 \\ f(x) & = 8 .\frac{1}{2} . [\cos (A+B) + \cos (A-B) ] + 3 \\ f(x) & = 4 [\cos (2x) + \cos (\frac{-\pi}{2}) ] + 3 \\ f(x) & = 4 [\cos (2x) + 0 ] + 3 \\ f(x) & = 4 \cos (2x) + 3 \end{align}$

$\spadesuit \,$ Menentukan nilai maksimum dan minimum fungsi

$\begin{align} f(x) & = 4 \cos (2x) + 3 \rightarrow P = 4 , \, c = 3 \\ a & = f_\text{maks} = |P| + c = |4| + 3 = 4+3 = 7 \\ b & = f_\text{min} = -|P| + c = -|4| + 3 = -4+3 = -1 \end{align}$
Sehingga nilai :

$a +b = 7 + (-1) = 6$

$\spadesuit \,$ Berdasarkan petunjuk B
Pernyataan pertama :

$a + b = 6 \,$ (benar)
Pernyataan kedua :

$a = -5 , \, b = 11 \,$ (salah , karena seharusnya

$a = 7, \, b=-1$ )
Karena pernyataan pertama benar dan pernyataan kedua salah, berdasarkan petunjuk B jawabannya adalah C.
Jadi, jawabannya C.

$\heartsuit$

Nomor 9

Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Jumlah

$n \,$ suku pertama suatu deret aritmetika dinyatakan dengan

$s_n = 2n^2 - n \,$ . Suku ke-12 deret tersebut adalah 45.
SEBAB
Deret tersebut mempunyai suku pertama

$a = 1 \,$ dan beda

$b = 4 .$

$\clubsuit \,$ Konsep Dasar Barisan aritmetika

$u_n = a+(n-1)b, \, \, u_n = s_n - s_{n-1} , \,$ dan

$b = u_n - u_{n-1}$

$\clubsuit \,$ Menentukan nilai

$a \,$ dan

$b$

$\begin{align} s_n & = 2n^2 - n \\ a & = u_1 = s_1 = 2.1^2 - 1 = 1 \\ u_2 & = s_2 - s_1 \\ u_2 & = (2.2^2 - 2) - 1 = 6 - 1 = 5 \\ b & = u_2 - u_1 = 5 - 1 = 4 \end{align}$
sehingga nilai

$a = 1 \,$ dan

$b = 4$

$\clubsuit \,$ Menentukan suku ke-12

$\begin{align} u_n & = a+(n-1)b \\ u_{12} & = 1+(12-1).4 \\ u_{12} & = 1+44 \\ u_{12} & = 45 \end{align}$
sehingga nilai

$u_{12} = 45$

$\clubsuit \,$ Berdasarkan petunjuk B
Pernyataan pertama :

$u_{12} = 45 \,$ (benar)
Pernyataan kedua :

$a = 1 \,$ dan

$b = 4 \,$ (benar)
Karena kedua pernyataan benar dan saling berhubungan, maka berdasarkan petunjuk B jawabannya A.
Jadi, jawabannya A.

$\heartsuit$

Nomor 10

Petunjuk B digunakan untuk menjawab soal nomor 8 dan 10.
Apabila

$a = 0 \,$ dan

$b \,$ sembarang, maka matriks

$\left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \,$ tidak mempunyai invers .
SEBAB
Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol.

$\spadesuit \,$ Konsep Matriks
*) Determinan

$A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow Det(A) = ad-bc$
*) Suatu matriks tidak mempunyai invers jika nilai determinannya sama dengan nol.

$\spadesuit \,$ Menentukan determinan matriksnya

$\begin{align} A & = \left( \begin{matrix} a & a + b \\ a-b & a \end{matrix} \right) \\ Det(A) & = a.a - (a-b)(a+b) \\ Det(A) & = a^2 - (a^2-b^2) \\ Det(A) & = b^2 \end{align}$
Karena nilai

$b \,$ sembarang, maka nilai

$Det(A) \,$ tidak selalu sama dengan nol, artinya Det(A) nilainya bisa nol atau tidak nol, sehingga matriks tersebut bisa mempunyai invers atau juga bisa tidak punya invers.

$\spadesuit \,$ Berdasarkan petunjuk B
Pernyataan pertama : Matriks tidak punya invers (salah)
Pernyataan kedua : Suatu matriks tidak punya invers jika nilai determinannya sama dengan nol. (Benar)
Karena pernyataan pertama salah dan pernyataan kedua benar, berdasarkan petunjuk B jawabannya D.
Jadi, jawabannya D.

$\heartsuit$

Nomor Soal Lainnya : 1-5 6-10 11-15

Tidak ada komentar:

Posting Komentar

Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.

dunia informa

Pages - Menu