Nomor 11
Petunjuk C digunakan untuk menjawab soal nomor 11 dan 15.
Jika α memenuhi persamaan sinx=√2cosx maka
(1). cosα=−1+√2
(2). sinα=√2+2√2
(3). tanα=√2√2−2−1+√2
(4). cosα=1−√2
Jika α memenuhi persamaan sinx=√2cosx maka
(1). cosα=−1+√2
(2). sinα=√2+2√2
(3). tanα=√2√2−2−1+√2
(4). cosα=1−√2
♣ Konsep dasar
*). identitas trigonometri
sin2x+cos2x=1→sin2x=1−cos2x
*). dari bentuk sinx=√2cosx , maka nilai sinx dan cosx positif.
♣ Menentukan nilai cosx
sinx=√2cosx(kuadratkan)sin2x=2cosx(gunakan identitas)1−cos2x=2cosxcos2x+2cosx−1=0Misalkan p=cosx>0p2+2p−1=0(gunakan rumus ABC)a=1,b=2,c=−1p=−b±√b2−4ac2ap=−2±√22−4.1.(−1)2.1p=−2±√82p=−2±2√22p=−1±√2
Karena nilai cosx positif, maka yang memenuhi adalah cosα=cosx=−1+√2
♣ Buat segitiga dari cosα=−1+√21=sami

Dari segitiga di atas diperoleh :
sinα=demi=√2√2−21=√2√2−2tanα=desa=√2√2−2−1+√2
Sehingga yang benar adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, jawabannya B. ♡
*). identitas trigonometri
sin2x+cos2x=1→sin2x=1−cos2x
*). dari bentuk sinx=√2cosx , maka nilai sinx dan cosx positif.
♣ Menentukan nilai cosx
sinx=√2cosx(kuadratkan)sin2x=2cosx(gunakan identitas)1−cos2x=2cosxcos2x+2cosx−1=0Misalkan p=cosx>0p2+2p−1=0(gunakan rumus ABC)a=1,b=2,c=−1p=−b±√b2−4ac2ap=−2±√22−4.1.(−1)2.1p=−2±√82p=−2±2√22p=−1±√2
Karena nilai cosx positif, maka yang memenuhi adalah cosα=cosx=−1+√2
♣ Buat segitiga dari cosα=−1+√21=sami

Dari segitiga di atas diperoleh :
sinα=demi=√2√2−21=√2√2−2tanα=desa=√2√2−2−1+√2
Sehingga yang benar adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, jawabannya B. ♡
Nomor 12
Petunjuk C digunakan untuk menjawab soal nomor 11 dan 15.
Jika gambar di bawah ini adalah grafik y=df(x)dx , maka dapat disimpulkan bahawa f(x)
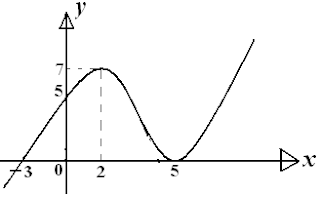
(1). mempunyai nilai minimum lokal pada x=−3
(2). turun pada interval x<−3
(3). mempunyai titik belok pada x=5
(4). mempunyai nilai maksimum lokal pada x=2
Jika gambar di bawah ini adalah grafik y=df(x)dx , maka dapat disimpulkan bahawa f(x)

(1). mempunyai nilai minimum lokal pada x=−3
(2). turun pada interval x<−3
(3). mempunyai titik belok pada x=5
(4). mempunyai nilai maksimum lokal pada x=2
♠ Konsep dasar turunan
f′(x)>0→ fungsi f(x) naik
f′(x)<0→ fungsi f(x) turun
♠ Dari gambar pada soal, akar-akarnya (titik potong sumbu X) adalah -3 dan 5, artinya f′(x)=0 akar-akarnya -3 dan 5. Untuk memudahkan menganalisa fungsi aslinya f(x) , kita gambar dulu garis bilangan turunannya f′(x) .
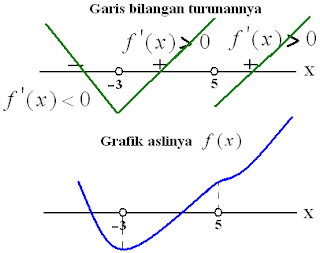
Keterangan grafik fungsi f(x) di atas :
*). mempunyai nilai minimum lokal pada x=−3
*). turun pada interval x<−3
*). mempunyai titik belok pada x=5
sehingga pernyataan yang benar adalah (1), (2), dan (3).
Jadi, pernyataan yang benar adalah (1), (2), dan (3). ♡
f′(x)>0→ fungsi f(x) naik
f′(x)<0→ fungsi f(x) turun
♠ Dari gambar pada soal, akar-akarnya (titik potong sumbu X) adalah -3 dan 5, artinya f′(x)=0 akar-akarnya -3 dan 5. Untuk memudahkan menganalisa fungsi aslinya f(x) , kita gambar dulu garis bilangan turunannya f′(x) .

Keterangan grafik fungsi f(x) di atas :
*). mempunyai nilai minimum lokal pada x=−3
*). turun pada interval x<−3
*). mempunyai titik belok pada x=5
sehingga pernyataan yang benar adalah (1), (2), dan (3).
Jadi, pernyataan yang benar adalah (1), (2), dan (3). ♡
Nomor 13
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Diketahui 2loga>1 dan 2logb>1, sedangkan a≠b. Hubungan antara a dan b yang berlaku adalah .....
(1). ab>1
(2). ba>1
(3). a−b>1
(4). a.b>4
Diketahui 2loga>1 dan 2logb>1, sedangkan a≠b. Hubungan antara a dan b yang berlaku adalah .....
(1). ab>1
(2). ba>1
(3). a−b>1
(4). a.b>4
♣ Konsep pertidaksamaan logaritma
clogf(x)>clogg(x)→f(x)>g(x)
dengan syarat : c>1 (basisnya > 1)
♣ Menentukan nilai a dan b
2loga>1→2loga>2log2a>2...(i)2logb>1→2logb>2log2b>2...(ii)
Dari (i) dan (ii) diperoleh :
a.b>2.2→a.b>4
sehingga yang benar adalah pernyataan (4), berdasarkan petunjuk C jawabannya D.
Jadi, jawabannya D. ♡
clogf(x)>clogg(x)→f(x)>g(x)
dengan syarat : c>1 (basisnya > 1)
♣ Menentukan nilai a dan b
2loga>1→2loga>2log2a>2...(i)2logb>1→2logb>2log2b>2...(ii)
Dari (i) dan (ii) diperoleh :
a.b>2.2→a.b>4
sehingga yang benar adalah pernyataan (4), berdasarkan petunjuk C jawabannya D.
Jadi, jawabannya D. ♡
Nomor 14
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Jika ¯p∨¯q adalah pernyataan benar, maka
(1). ¯p∧q benar
(2). ¯q⇒p benar
(3). ¯p⇔¯q benar
(4). ¯p∧¯q salah
Jika ¯p∨¯q adalah pernyataan benar, maka
(1). ¯p∧q benar
(2). ¯q⇒p benar
(3). ¯p⇔¯q benar
(4). ¯p∧¯q salah
♠ Tabel kebenaran logika matematika

Keterangan : B = Benar dan S = Salah
♠ Untuk menyelesaiakan soal ini, kita langsung menggunakan tabel kebenarannya
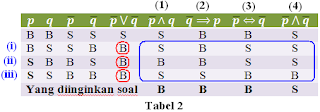
¯p∨¯q adalah pernyataan benar, sehingga yang digunakan hanya baris yang nilai ¯p∨¯q juga benar (lihat kolom ¯p∨¯q yang kolomnya dilingkari merah) yaitu baris (i), (ii), dan (iii) yang diberi warna biru.
♠ Berdasarkan petunjuk C, yang diinginkan soal : BBBS
Kita cocokkan ketiga baris yang memenuhi, dan kalau ada yang sama maka diinggap benar. Cuma perhatikan 4 kolom yang diberi kotak biru saja, kemudian samakan dengan yang diinginkan soal yaitu : BBBS .
Baris (i) , Hasilnya SBSS , yang sama pernyataan (2) dan (4), bedasarkan petunjuk C jawabannya C
Baris (ii) , Hasilnya BBSS , yang sama pernyataan (1), (2) dan (4), bedasarkan petunjuk C tidak ada jawabannya
Baris (iii) , Hasilnya SSBB , yang sama pernyataan (3) saja, bedasarkan petunjuk C tidak ada jawabannya
Sehingga yang benar dan cocok dengan petunjuk C adalah barisan (i) yang jawabannya C.
Jadi, pernyataan yang sama adalah (2), dan (4), jawabannya C. ♡

Keterangan : B = Benar dan S = Salah
♠ Untuk menyelesaiakan soal ini, kita langsung menggunakan tabel kebenarannya

¯p∨¯q adalah pernyataan benar, sehingga yang digunakan hanya baris yang nilai ¯p∨¯q juga benar (lihat kolom ¯p∨¯q yang kolomnya dilingkari merah) yaitu baris (i), (ii), dan (iii) yang diberi warna biru.
♠ Berdasarkan petunjuk C, yang diinginkan soal : BBBS
Kita cocokkan ketiga baris yang memenuhi, dan kalau ada yang sama maka diinggap benar. Cuma perhatikan 4 kolom yang diberi kotak biru saja, kemudian samakan dengan yang diinginkan soal yaitu : BBBS .
Baris (i) , Hasilnya SBSS , yang sama pernyataan (2) dan (4), bedasarkan petunjuk C jawabannya C
Baris (ii) , Hasilnya BBSS , yang sama pernyataan (1), (2) dan (4), bedasarkan petunjuk C tidak ada jawabannya
Baris (iii) , Hasilnya SSBB , yang sama pernyataan (3) saja, bedasarkan petunjuk C tidak ada jawabannya
Sehingga yang benar dan cocok dengan petunjuk C adalah barisan (i) yang jawabannya C.
Jadi, pernyataan yang sama adalah (2), dan (4), jawabannya C. ♡
Nomor 15
Petunjuk C digunakan untuk menjawab soal nomor 11 sampai 15.
Interval yang memenuhi pertidaksamaan x−1≤2x adalah ....
(1). x≤−1
(2). −1≤x<0
(3). 0<x≤2
(4). −1≤x≤2,x≠0
Interval yang memenuhi pertidaksamaan x−1≤2x adalah ....
(1). x≤−1
(2). −1≤x<0
(3). 0<x≤2
(4). −1≤x≤2,x≠0
♣ Menyelesaikan pertidaksamaannya
x−1≤2x(x−1)−2x≤0x(x−1)−2x≤0x2−x−2x≤0(x+1)(x−2)x≤0x=−1,x=2,x=0

Solusinya : HP={x≤−1∨0<x≤2}
Sehingga pernyataan yang benar sesuai dengan solusi di atas adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, yang benar pernyataan (1) dan (3), jawabannya B. ♡
x−1≤2x(x−1)−2x≤0x(x−1)−2x≤0x2−x−2x≤0(x+1)(x−2)x≤0x=−1,x=2,x=0

Solusinya : HP={x≤−1∨0<x≤2}
Sehingga pernyataan yang benar sesuai dengan solusi di atas adalah pernyataan (1) dan (3), berdasarkan petunjuk C jawabannya B.
Jadi, yang benar pernyataan (1) dan (3), jawabannya B. ♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.