Nomor 11
Misalkan l1 dan l2 menyatakan garis yang menyinggung lingkaran x2+y2=r2 berturut-turut di
P1(x1,y1) dan P2(x2,y2) . Jika l1 dan l2 berpotongan di (2,−1) dan titik (4,−1)
berada pada garis yang melalui P1 dan P2 , maka r=.....
♣ Gambar
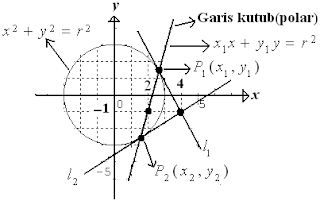
Dari gambar di atas, garis yang menghubungkan titik P1 dan P2 disebut garis kutub(polar) dengan persamaan x1x+y1y=r2 yang dibentuk dari kedua garis singgung lingkaran l1 dan l2 yang berpotongan di titik (4,-1).
Persamaan garis kutub dari titik (4,-1) adalah
x1x+y1y=r2→4x−y=r2
♣ Menentukan nilai r dengan substitusi titik (2,-1) ke persamaan garis kutub (garis kutub melalui titik (2,-1) ).
(x,y)=(2,−1)→4x−y=r24.2−(−1)=r28+1=r29=r2r=3
Jadi, nilai r=3.♡
Catatan : Dari soal, sebenarnya kedua garis singgung berpotongan di titik (2,-1) , akan tetapi itu tidak mungkin karena gambar lingkarannya akan semakin kecil sehingga garis kutubnya tidak mungkin melalui titik (4,-1). Maka dari itu, kasusnya di balik yaituu kedua garis singgung berpotongan di titik (4,-1) dan garis kutub melalui titik (2,-1) seperti gambar di atas. Ini artinya ada kesalahan pengetikan pada soal.

Dari gambar di atas, garis yang menghubungkan titik P1 dan P2 disebut garis kutub(polar) dengan persamaan x1x+y1y=r2 yang dibentuk dari kedua garis singgung lingkaran l1 dan l2 yang berpotongan di titik (4,-1).
Persamaan garis kutub dari titik (4,-1) adalah
x1x+y1y=r2→4x−y=r2
♣ Menentukan nilai r dengan substitusi titik (2,-1) ke persamaan garis kutub (garis kutub melalui titik (2,-1) ).
(x,y)=(2,−1)→4x−y=r24.2−(−1)=r28+1=r29=r2r=3
Jadi, nilai r=3.♡
Catatan : Dari soal, sebenarnya kedua garis singgung berpotongan di titik (2,-1) , akan tetapi itu tidak mungkin karena gambar lingkarannya akan semakin kecil sehingga garis kutubnya tidak mungkin melalui titik (4,-1). Maka dari itu, kasusnya di balik yaituu kedua garis singgung berpotongan di titik (4,-1) dan garis kutub melalui titik (2,-1) seperti gambar di atas. Ini artinya ada kesalahan pengetikan pada soal.
Nomor 12
Bila sin(40∘+x)=a,0∘<x<45∘, maka cos(70∘+x)=....
♠ gambar dari sin(40∘+x)=a=a1=demi

Sehingga nilai cos(40∘+x)=√1−a21=√1−a2
Konsep dasar : cos(A+B)=cosAcosB−sinAsinB
♠ Menentukan nilai cos(70∘+x)
cos(70∘+x)=cos[(30∘)+(40∘+x)]=cos30∘cos(40∘+x)−sin30∘sin(40∘+x)=12√3.√1−a2−12.a=12√3(1−a2)−12acos(70∘+x)=√3(1−a2)−a2
Jadi, nilai cos(70∘+x)=√3(1−a2)−a2.♡

Sehingga nilai cos(40∘+x)=√1−a21=√1−a2
Konsep dasar : cos(A+B)=cosAcosB−sinAsinB
♠ Menentukan nilai cos(70∘+x)
cos(70∘+x)=cos[(30∘)+(40∘+x)]=cos30∘cos(40∘+x)−sin30∘sin(40∘+x)=12√3.√1−a2−12.a=12√3(1−a2)−12acos(70∘+x)=√3(1−a2)−a2
Jadi, nilai cos(70∘+x)=√3(1−a2)−a2.♡
Nomor 13
Jika A[10]=[24], dan
A[−12]=[−5−6],
maka A[2−506]=....
♠ Misalkan matriks A=[abcd]
♠ Menentukan matriks A dengan menyelesaikan persamaan
A[10]=[24](dari pers(i))[abcd][10]=[24][ac]=[24]a=2 dan c=4A[−12]=[−5−6](dari pers(ii))[2b4d][−12]=[−5−6][−2+2b−4+2d]=[−5−6]−2+2b=−5→b=−32−4+2d=−6→d=−1
Sehingga matriks A=[2−324−1]
♠ Menentukan hasil perkaliannya
A[2−506]=[2−324−1].[2−506]=[4−198−26]
Jadi, nilai A[2−506]=[4−198−26].♡
♠ Menentukan matriks A dengan menyelesaikan persamaan
A[10]=[24](dari pers(i))[abcd][10]=[24][ac]=[24]a=2 dan c=4A[−12]=[−5−6](dari pers(ii))[2b4d][−12]=[−5−6][−2+2b−4+2d]=[−5−6]−2+2b=−5→b=−32−4+2d=−6→d=−1
Sehingga matriks A=[2−324−1]
♠ Menentukan hasil perkaliannya
A[2−506]=[2−324−1].[2−506]=[4−198−26]
Jadi, nilai A[2−506]=[4−198−26].♡
Nomor 14
Misalkan A(t) menyatakan luas daerah di bawah kurva y=bx2,0≤x≤t. Jika titik P(x0,0) sehingga A(x0):A(1)=1:8, maka perbandingan
luas trapesium ABPQ:DCPQ=...


♠ Menentukan A(t):
A(t)=∫t0bx2dx=[b3x3]t0=b3(t3−03)A(t)=b3t3t=x0→A(x0)=b3(x0)3t=1→A(1)=b3(1)3=b3
♠ Menentukan x0 dari A(x0):A(1)=1:8
A(x0)A(1)=18⇒b3(x0)3b3=18⇒x30=18⇒x0=12
♠ Menentukan titik A, Q, dan D dengan menggunakan y=bx2
titik A : x=−1⇒y=b(−1)2=b. Jadi titik A(-1, b)
titik Q : x=12⇒y=b(12)2=b. Jadi titik Q(1/2, b/4)
titik D : x=1⇒y=b(1)2=b. Jadi titik D(1, b)

♠ Menentukan perbandingan luas ABPQ:DCPQ
L.ABPQL.DCPQ=12(AB+PQ).BP12(CD+PQ).CP=(b+b4).32(b+b4).12=31
Jadi, perbandingan luas L.ABPQL.DCPQ=31.♡
A(t)=∫t0bx2dx=[b3x3]t0=b3(t3−03)A(t)=b3t3t=x0→A(x0)=b3(x0)3t=1→A(1)=b3(1)3=b3
♠ Menentukan x0 dari A(x0):A(1)=1:8
A(x0)A(1)=18⇒b3(x0)3b3=18⇒x30=18⇒x0=12
♠ Menentukan titik A, Q, dan D dengan menggunakan y=bx2
titik A : x=−1⇒y=b(−1)2=b. Jadi titik A(-1, b)
titik Q : x=12⇒y=b(12)2=b. Jadi titik Q(1/2, b/4)
titik D : x=1⇒y=b(1)2=b. Jadi titik D(1, b)

♠ Menentukan perbandingan luas ABPQ:DCPQ
L.ABPQL.DCPQ=12(AB+PQ).BP12(CD+PQ).CP=(b+b4).32(b+b4).12=31
Jadi, perbandingan luas L.ABPQL.DCPQ=31.♡
Nomor 15
Semua nilai x yang memenuhi pertidaksamaan |1−x|log(x+5)>2 adalah ....
♠ Konsep Dasar
Definisi harga mutlak : |f(x)|2=(f(x))2
f(x)log[g(x)]=h(x) syarat logaritma : f(x)>0,f(x)≠1,g(x)>0
Pertidaksamaan Logaritma :
f(x)log[g(x)]>f(x)log[h(x)] memiliki solusi berdasarkan basisnya
untuk 0<f(x)<1 solusinya g(x)<h(x) (tanda dibalik)
untuk f(x)>1 solusinya g(x)>h(x) (tanda tidak dibalik)
♠ Menentukan syarat logaritmanya
|1−x|log(x+5)>2 memiliki syarat :
syarat basis : |1−x|>0→x∈R,x≠1
|1−x|≠1→x≠0,x≠2
syarat numerus : (x+5)>0→x>−5
Sehingga syarat totalnya : HP1 = {x>−5,x≠0,x≠1,x≠2}
♠ Menyelesaikan pertidaksamaan berdasarkan basisnya yang dibagi menjadi dua kasus
*). untuk 0<|1−x|<1→{0<x<2} (tanda dibalik)
|1−x|log(x+5)>2|1−x|log(x+5)>|1−x|log|1−x|2(x+5)<|1−x|2(x+5)<(1−x)2x+5<x2−2x+1−x2+3x+4<0(−x+4)(x+1)<0x=4∨x=−1

pada garis bilangan yang diminta negatif ( < 0 ), solusinya {x<−1∨x>4}
dari {0<x<2} dan {x<−1∨x>4} maka pada kasus ini tidak ada nilai x yang memenuhi.
**). untuk |1−x|>1→{x<0∨x>2} (tanda tidak dibalik)
|1−x|log(x+5)>2|1−x|log(x+5)>|1−x|log|1−x|2(x+5)>|1−x|2(x+5)>(1−x)2x+5>x2−2x+1−x2+3x+4>0(−x+4)(x+1)>0x=4∨x=−1
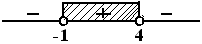
pada garis bilangan yang diminta positif ( > 0 ), solusinya {−1<x<4}
dari {x<0∨x>2} dan {−1<x<4} maka pada kasus ini solusinya adalah HP2={−1<x<0∨2<x<4}
Sehingga solusi totalnya :
HP=HP1∩HP2={−1<x<0∨2<x<4}
Jadi, semua nilai x nya adalah {−1<x<0∨2<x<4}.♡
Definisi harga mutlak : |f(x)|2=(f(x))2
f(x)log[g(x)]=h(x) syarat logaritma : f(x)>0,f(x)≠1,g(x)>0
Pertidaksamaan Logaritma :
f(x)log[g(x)]>f(x)log[h(x)] memiliki solusi berdasarkan basisnya
untuk 0<f(x)<1 solusinya g(x)<h(x) (tanda dibalik)
untuk f(x)>1 solusinya g(x)>h(x) (tanda tidak dibalik)
♠ Menentukan syarat logaritmanya
|1−x|log(x+5)>2 memiliki syarat :
syarat basis : |1−x|>0→x∈R,x≠1
|1−x|≠1→x≠0,x≠2
syarat numerus : (x+5)>0→x>−5
Sehingga syarat totalnya : HP1 = {x>−5,x≠0,x≠1,x≠2}
♠ Menyelesaikan pertidaksamaan berdasarkan basisnya yang dibagi menjadi dua kasus
*). untuk 0<|1−x|<1→{0<x<2} (tanda dibalik)
|1−x|log(x+5)>2|1−x|log(x+5)>|1−x|log|1−x|2(x+5)<|1−x|2(x+5)<(1−x)2x+5<x2−2x+1−x2+3x+4<0(−x+4)(x+1)<0x=4∨x=−1

pada garis bilangan yang diminta negatif ( < 0 ), solusinya {x<−1∨x>4}
dari {0<x<2} dan {x<−1∨x>4} maka pada kasus ini tidak ada nilai x yang memenuhi.
**). untuk |1−x|>1→{x<0∨x>2} (tanda tidak dibalik)
|1−x|log(x+5)>2|1−x|log(x+5)>|1−x|log|1−x|2(x+5)>|1−x|2(x+5)>(1−x)2x+5>x2−2x+1−x2+3x+4>0(−x+4)(x+1)>0x=4∨x=−1

pada garis bilangan yang diminta positif ( > 0 ), solusinya {−1<x<4}
dari {x<0∨x>2} dan {−1<x<4} maka pada kasus ini solusinya adalah HP2={−1<x<0∨2<x<4}
Sehingga solusi totalnya :
HP=HP1∩HP2={−1<x<0∨2<x<4}
Jadi, semua nilai x nya adalah {−1<x<0∨2<x<4}.♡
Terimakasih, sangat bermanfaat.
BalasHapusHallow @Faida,
HapusSama-sama.
Terima kasih untuk kunjungannya ke blog dunia informa ini.
Semoga terus bisa membantu.
req no. 40 min
BalasHapusHallow,
HapusTerimakasih untuk kunjungannya ke blog dunia-informa ini.
kami kurang mengerti maksud pernyataan "req no. 40"?