Nomor 6
Diketahui vektor satuan →u=0,8→i+a→j. Jika vektor →v=b→i+→j
tegak lurus →u , maka a.b=....
♠ Konsep dasar
Panjang vektor →u=a→i+b→j→panjang =|→u|=√a2+b2
→u vektor satuan, sehingga |→u|=1
→u tegak lurus →v , sehingga →u.→v=0
♠ Menentukan nilai a
→u=0,8→i+a→j vektor satuan, sehingga
|→u|=1→√(0,8)2+a2=10,64+a2=1a2=0,36a=0,6
♠ Menentukan nilai b
→u tegak lurus →v sehingga →u.→v=0
dengan →u=0,8→i+a→j dan →v=b→i+→j
→u.→v=00,8.b+a.1=00,8b+0,6.1=00,8b=−0,6→b=−0,60,8=−34
Sehingga nilai a.b=(0,6).(−34)=(35).(−34)=−920
Jadi, nilai a.b=−920.♡
Panjang vektor →u=a→i+b→j→panjang =|→u|=√a2+b2
→u vektor satuan, sehingga |→u|=1
→u tegak lurus →v , sehingga →u.→v=0
♠ Menentukan nilai a
→u=0,8→i+a→j vektor satuan, sehingga
|→u|=1→√(0,8)2+a2=10,64+a2=1a2=0,36a=0,6
♠ Menentukan nilai b
→u tegak lurus →v sehingga →u.→v=0
dengan →u=0,8→i+a→j dan →v=b→i+→j
→u.→v=00,8.b+a.1=00,8b+0,6.1=00,8b=−0,6→b=−0,60,8=−34
Sehingga nilai a.b=(0,6).(−34)=(35).(−34)=−920
Jadi, nilai a.b=−920.♡
Nomor 7
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2. Jika P titik tengah HG, Q titik tengah FG, R titik tengah PQ, dan BS
adalah proyeksi BR pada bidang ABCD, maka panjang BS adalah .....
♣ Gambar

Proyeksi BR pada ABCD adalah BS.
BM=12BD=12.2√2=√2
MS=12MC=12√2
♣ Menentukan panjang BS pada ΔBMS
BS=√BM2+MS2=√(√2)2+(12√2)2=√4+12=√52=√5√2.√2√2=12√10
Jadi, panjang BS=12√10.♡

Proyeksi BR pada ABCD adalah BS.
BM=12BD=12.2√2=√2
MS=12MC=12√2
♣ Menentukan panjang BS pada ΔBMS
BS=√BM2+MS2=√(√2)2+(12√2)2=√4+12=√52=√5√2.√2√2=12√10
Jadi, panjang BS=12√10.♡
Nomor 8
Jika lingkaran x2+y2+6x+6y+c=0 menyinggung garis x=2,
maka nilai c adalah .....
♠ Substitusi x=2 ke persamaan lingkaran
x=2→x2+y2+6x+6y+c=022+y2+6.2+6y+c=0y2+6y+(c+16)=0
Syarat Menyinggung : D=0
b2−4ac=062−4.1.(c+16)=036−4c−64=04c=−28c=−7
Jadi, nilai c=−7.♡
x=2→x2+y2+6x+6y+c=022+y2+6.2+6y+c=0y2+6y+(c+16)=0
Syarat Menyinggung : D=0
b2−4ac=062−4.1.(c+16)=036−4c−64=04c=−28c=−7
Jadi, nilai c=−7.♡
Nomor 9
Himpunan penyelesaian |x2−2|≤1 adalah himpunan nilai x yang memenuhi .....
♣ Konsep dasar : |x|2=x2 dan p2−q2=(p−q)(p+q)
♣ Kuadratkan kedua ruas
|x2−2|2≤12(x2−2)2≤12(x2−2)2−12≤0[x2−2−1][x2−2+1]≤0(x2−3)(x2−1)≤0x2−3=0→x2=3→x=±√3x2−1=0→x2=1→x=±1
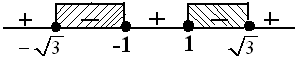
Jadi, solusinya HP={−√3≤x≤−1∨1≤x≤√3}.♡
♣ Kuadratkan kedua ruas
|x2−2|2≤12(x2−2)2≤12(x2−2)2−12≤0[x2−2−1][x2−2+1]≤0(x2−3)(x2−1)≤0x2−3=0→x2=3→x=±√3x2−1=0→x2=1→x=±1
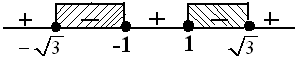
Jadi, solusinya HP={−√3≤x≤−1∨1≤x≤√3}.♡
Nomor 10
limx→1(x2+x−2)sin(x−1)x2−2x+1=.....
♠ Konsep dasar limit
limx→ksinaf(x)bf(x)=ab dengan syarat f(k)=0
♠ Menyelesaikan limitnya
limx→1(x2+x−2)sin(x−1)x2−2x+1=limx→1(x+2)(x−1)sin(x−1)(x−1)(x−1)=limx→1(x+2)sin(x−1)(x−1)=limx→1(x+2).sin(x−1)(x−1)=(1+2).11=3
Jadi, nilai limitnya adalah 3. ♡
limx→ksinaf(x)bf(x)=ab dengan syarat f(k)=0
♠ Menyelesaikan limitnya
limx→1(x2+x−2)sin(x−1)x2−2x+1=limx→1(x+2)(x−1)sin(x−1)(x−1)(x−1)=limx→1(x+2)sin(x−1)(x−1)=limx→1(x+2).sin(x−1)(x−1)=(1+2).11=3
Jadi, nilai limitnya adalah 3. ♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.