Nomor 6
Diketahui sin(40∘+α)=b, dengan 0<α<50∘. Nilai dari cos(10∘+α)=...
♠ Buat segitiga dari sin(40∘+α)=b1=demi
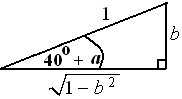
Sehingga : cos(40∘+α)=√1−b21=√1−b2
♠ Konsep : cos(A−B)=cosAcosB+sinAsinB
♠ Menentukan cos(10∘+α)
cos(10∘+α)=cos[(40∘+α)−(30∘)]=cos(40∘+α).cos30∘+sin(40∘+α).sin30∘=√1−b2.12√3+b.12=12(√3(1−b2)+b)
Jadi, nilai cos(10∘+α)=12(√3(1−b2)+b).♡
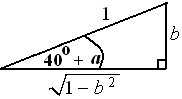
Sehingga : cos(40∘+α)=√1−b21=√1−b2
♠ Konsep : cos(A−B)=cosAcosB+sinAsinB
♠ Menentukan cos(10∘+α)
cos(10∘+α)=cos[(40∘+α)−(30∘)]=cos(40∘+α).cos30∘+sin(40∘+α).sin30∘=√1−b2.12√3+b.12=12(√3(1−b2)+b)
Jadi, nilai cos(10∘+α)=12(√3(1−b2)+b).♡
Nomor 7
Banyaknya nilai x dengan 0≤x≤2014π yang memenuhi persamaan sin3x3−4sin2x=1 adalah ...
♣ Syarat penyebut pecahan sin3x3−4sin2x=1
3−4sin2x≠→sin2x≠34 ....(i)
♣ Konsep dasar
sin3x=3sinx−4sin3x
♣ Misal p=sinx , menyelesaikan persamaan
sin3x3−4sin2x=1sin3x=3−4sin2x3sinx−4sin3x=3−4sin2x4sin3x−4sin2x−3sinx+3=04p3−4p2−3p+3=0dengan skema horner diperoleh(4p2−3)(p−1)=0p2=34∨p=1
Skema hornernya :
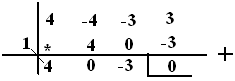
Untuk p2=34→sin2x=34, berdasarkan (i) maka sin2x=34 tidak memenuhi .
Untuk p=1→sinx=1→sinx=sinπ2
solusinya :
x=θ+k.2πx=π2+k.2π...(1) atau x=θ+k.2πx=(180∘−π2)+k.2πx=π2+k.2π...(2)
Bentuk (1) dan (2) sama, sehingga diambil salah satu saja.
x=π2+k.2π→x=(2k+12)π ...(ii)
♣ Menentukan banyaknya solusi dari bentuk (ii) dan syarat 0≤x≤2014π
0≤x≤2014π0≤(2k+12)π≤2014π(bagi π)0≤2k+12≤2014−12≤2k≤2014−12(bagi 2)−14≤k≤1007−14−14≤k≤1006+34karena k bulat, maka 0≤k≤1006
Ada 1007 bilangan bulat k yang memenuhi, sehingga solusi x berdasarkan x=(2k+12)π juga ada 1007 solusi.
Jadi, banyaknya x yang memenuhi ada 1007 bilangan. ♡
3−4sin2x≠→sin2x≠34 ....(i)
♣ Konsep dasar
sin3x=3sinx−4sin3x
♣ Misal p=sinx , menyelesaikan persamaan
sin3x3−4sin2x=1sin3x=3−4sin2x3sinx−4sin3x=3−4sin2x4sin3x−4sin2x−3sinx+3=04p3−4p2−3p+3=0dengan skema horner diperoleh(4p2−3)(p−1)=0p2=34∨p=1
Skema hornernya :
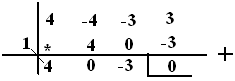
Untuk p2=34→sin2x=34, berdasarkan (i) maka sin2x=34 tidak memenuhi .
Untuk p=1→sinx=1→sinx=sinπ2
solusinya :
x=θ+k.2πx=π2+k.2π...(1) atau x=θ+k.2πx=(180∘−π2)+k.2πx=π2+k.2π...(2)
Bentuk (1) dan (2) sama, sehingga diambil salah satu saja.
x=π2+k.2π→x=(2k+12)π ...(ii)
♣ Menentukan banyaknya solusi dari bentuk (ii) dan syarat 0≤x≤2014π
0≤x≤2014π0≤(2k+12)π≤2014π(bagi π)0≤2k+12≤2014−12≤2k≤2014−12(bagi 2)−14≤k≤1007−14−14≤k≤1006+34karena k bulat, maka 0≤k≤1006
Ada 1007 bilangan bulat k yang memenuhi, sehingga solusi x berdasarkan x=(2k+12)π juga ada 1007 solusi.
Jadi, banyaknya x yang memenuhi ada 1007 bilangan. ♡
Nomor 8
Jika lim
\spadesuit \, Menentukan nilai limit masing-masing
Konsep : \left( \frac{a}{b} \right)^{-1} = \frac{b}{a}
\begin{align} & \displaystyle \lim_{x \to 1} \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4}{x(x-1)} -\frac{4-3x+x^2}{-(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4(x^2+x+1)}{x(x-1)(x^2+x+1)} + \frac{x(4-3x+x^2)}{(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4x^2+4x+4+4x-3x^2+x^3}{x(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{x^3+x^2+8x+4}{x^4-x} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \frac{x^4-x}{x^3+x^2+8x+4} \\ & = \frac{1^4-1}{1^3+1^2+8.1+4} = \frac{0}{14} = 0 \end{align}
Konsep Turunan pada limit:
\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{0}{0} \rightarrow \lim_{x \to a} \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to a} \frac{f^\prime (x)}{g^\prime (x)}
diturunkan sampai hasilnya tidak sama dengan \frac{0}{0}
\begin{align} & \displaystyle \lim_{x \to 1} \frac{4(x^4-1)}{x^2-x^{-1}} = \frac{0}{0} \, \, \, \text{(diturunkan)} \\ & = \displaystyle \lim_{x \to 1} \frac{4(x^3)}{2x+\frac{1}{x^2}} \\ & = \frac{4(1^3)}{2.1+\frac{1}{1^2}} \\ & = \frac{16}{3} \end{align}
\spadesuit \, Menentukan hasil limitnya
\begin{align} & \displaystyle \lim_{x \to 1} \left[ \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1}+ \frac{4(x^4-1)}{x^2-x^{-1}} \right] \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1} + \displaystyle \lim_{x \to 1} \frac{4(x^4-1)}{x^2-x^{-1}} \\ & = 0 + \frac{16}{3} \\ & = \frac{16}{3} \end{align}
Jadi, nilai limitnya adalah \frac{16}{3} . \heartsuit
Konsep : \left( \frac{a}{b} \right)^{-1} = \frac{b}{a}
\begin{align} & \displaystyle \lim_{x \to 1} \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4}{x(x-1)} -\frac{4-3x+x^2}{-(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4(x^2+x+1)}{x(x-1)(x^2+x+1)} + \frac{x(4-3x+x^2)}{(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4x^2+4x+4+4x-3x^2+x^3}{x(x-1)(x^2+x+1)} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \left( \frac{x^3+x^2+8x+4}{x^4-x} \right)^{-1} \\ & = \displaystyle \lim_{x \to 1} \frac{x^4-x}{x^3+x^2+8x+4} \\ & = \frac{1^4-1}{1^3+1^2+8.1+4} = \frac{0}{14} = 0 \end{align}
Konsep Turunan pada limit:
\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{0}{0} \rightarrow \lim_{x \to a} \frac{f(x)}{g(x)} = \displaystyle \lim_{x \to a} \frac{f^\prime (x)}{g^\prime (x)}
diturunkan sampai hasilnya tidak sama dengan \frac{0}{0}
\begin{align} & \displaystyle \lim_{x \to 1} \frac{4(x^4-1)}{x^2-x^{-1}} = \frac{0}{0} \, \, \, \text{(diturunkan)} \\ & = \displaystyle \lim_{x \to 1} \frac{4(x^3)}{2x+\frac{1}{x^2}} \\ & = \frac{4(1^3)}{2.1+\frac{1}{1^2}} \\ & = \frac{16}{3} \end{align}
\spadesuit \, Menentukan hasil limitnya
\begin{align} & \displaystyle \lim_{x \to 1} \left[ \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1}+ \frac{4(x^4-1)}{x^2-x^{-1}} \right] \\ & = \displaystyle \lim_{x \to 1} \left( \frac{4}{x^2-x} -\frac{4-3x+x^2}{1-x^3} \right)^{-1} + \displaystyle \lim_{x \to 1} \frac{4(x^4-1)}{x^2-x^{-1}} \\ & = 0 + \frac{16}{3} \\ & = \frac{16}{3} \end{align}
Jadi, nilai limitnya adalah \frac{16}{3} . \heartsuit
Nomor 9
Misalkan f(0)=1 dan f^\prime(0)=2. Jika g(x)=\cos (f(x)), maka g^\prime(0)=...
\clubsuit \, Konsep dasar turunan
y = f[g(x)] \rightarrow y^\prime = f^\prime [g(x)] . g^\prime (x)
\clubsuit \, Menentukan turunan fungsi dan substitusi x = 0
\begin{align} g(x) & =\cos (f(x)) \\ g^\prime (x) & = f^\prime (x) . [-\sin (f(x)) ] \\ x=0 \rightarrow g^\prime (0) & = - f^\prime (0) . \sin (f(0)) \\ g^\prime (0) & = - 2 . \sin (1) \\ g^\prime (0) & = - 2 \sin 1 \end{align}
Jadi, nilai turunannya g^\prime (0) = - 2 \sin 1 . \heartsuit
y = f[g(x)] \rightarrow y^\prime = f^\prime [g(x)] . g^\prime (x)
\clubsuit \, Menentukan turunan fungsi dan substitusi x = 0
\begin{align} g(x) & =\cos (f(x)) \\ g^\prime (x) & = f^\prime (x) . [-\sin (f(x)) ] \\ x=0 \rightarrow g^\prime (0) & = - f^\prime (0) . \sin (f(0)) \\ g^\prime (0) & = - 2 . \sin (1) \\ g^\prime (0) & = - 2 \sin 1 \end{align}
Jadi, nilai turunannya g^\prime (0) = - 2 \sin 1 . \heartsuit
Nomor 10
Jika \int \limits_{-1}^a \frac{x+1}{(x+2)^4} \, dx=\frac{10}{81} dan a > -2, maka a=...
\spadesuit \, Konsep dasar integral
\int (ax+b)^n \, dx = \frac{1}{a}. \frac{1}{n+1}.(ax+b){n+1} + c
\spadesuit \, Menentukan integral dan nilai a
\begin{align} \int \limits_{-1}^a \frac{x+1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a \frac{(x+2)}{(x+2)^4} - \frac{1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a \frac{1}{(x+2)^3} - \frac{1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a (x+2)^{-3} - (x+2)^{-4} \, dx & = \frac{10}{81} \\ \left[ \frac{1}{1}. \frac{1}{-3+1}.(x+2)^{-3+1} - \frac{1}{1}. \frac{1}{-4+1}.(x+2)^{-4+1} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{-2}.(x+2)^{-2} - \frac{1}{-3}.(x+2)^{-3} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{-1}{2(x+2)^2} + \frac{1}{3(x+2)^3} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{3(x+2)^3} - \frac{1}{2(x+2)^2} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] - \left[ \frac{1}{3(-1+2)^3} - \frac{1}{2(-1+2)^2} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] - \left[ - \frac{1}{6} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] + \left[ \frac{1}{6} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] = \frac{10}{81} & - \frac{1}{6} \\ \text{(kedua ruas disederhanankan)} & \\ \frac{3a+4}{6(a+2)^3} & = \frac{7}{162} \end{align}
Sehingga : 3a + 4 = 7 \rightarrow a = 1
Jadi, nilai a = 1. \heartsuit
\int (ax+b)^n \, dx = \frac{1}{a}. \frac{1}{n+1}.(ax+b){n+1} + c
\spadesuit \, Menentukan integral dan nilai a
\begin{align} \int \limits_{-1}^a \frac{x+1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a \frac{(x+2)}{(x+2)^4} - \frac{1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a \frac{1}{(x+2)^3} - \frac{1}{(x+2)^4} \, dx & = \frac{10}{81} \\ \int \limits_{-1}^a (x+2)^{-3} - (x+2)^{-4} \, dx & = \frac{10}{81} \\ \left[ \frac{1}{1}. \frac{1}{-3+1}.(x+2)^{-3+1} - \frac{1}{1}. \frac{1}{-4+1}.(x+2)^{-4+1} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{-2}.(x+2)^{-2} - \frac{1}{-3}.(x+2)^{-3} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{-1}{2(x+2)^2} + \frac{1}{3(x+2)^3} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{3(x+2)^3} - \frac{1}{2(x+2)^2} \right]_{-1}^a & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] - \left[ \frac{1}{3(-1+2)^3} - \frac{1}{2(-1+2)^2} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] - \left[ - \frac{1}{6} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] + \left[ \frac{1}{6} \right] & = \frac{10}{81} \\ \left[ \frac{1}{3(a+2)^3} - \frac{1}{2(a+2)^2} \right] = \frac{10}{81} & - \frac{1}{6} \\ \text{(kedua ruas disederhanankan)} & \\ \frac{3a+4}{6(a+2)^3} & = \frac{7}{162} \end{align}
Sehingga : 3a + 4 = 7 \rightarrow a = 1
Jadi, nilai a = 1. \heartsuit
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.