Nomor 11
Nilai cos2π7+cos4π7+cos6π7=....
♣ Konsep trigonometri : 2cosxsiny=sin(x+y)−sin(x−y)
♣ Menyelesaikan soal dengan permisalan : x=π7
Modifikasi soal dengan mengalikannya dengan 2sinx2sinx agar mengarah ke rumus dasar di atas.
cos2π7+cos4π7+cos6π7=cos2x+cos4x+cos6x=(cos2x+cos4x+cos6x).2sinx2sinx=2cos2xsinx+2cos4x.sinx+2cos6x.sinx2sinx=(sin3x−sinx)+(sin5x−sin3x)+(sin7x−sin5x)2sinx=sin7x−sinx2sinx (substitusi x=π7)=sin7.π7−sinπ72sinπ7=sinπ−sinπ72sinπ7=0−sinπ72sinπ7=−sinπ72sinπ7=−12
Jadi, nilai cos2π7+cos4π7+cos6π7=−12.♡
♣ Menyelesaikan soal dengan permisalan : x=π7
Modifikasi soal dengan mengalikannya dengan 2sinx2sinx agar mengarah ke rumus dasar di atas.
cos2π7+cos4π7+cos6π7=cos2x+cos4x+cos6x=(cos2x+cos4x+cos6x).2sinx2sinx=2cos2xsinx+2cos4x.sinx+2cos6x.sinx2sinx=(sin3x−sinx)+(sin5x−sin3x)+(sin7x−sin5x)2sinx=sin7x−sinx2sinx (substitusi x=π7)=sin7.π7−sinπ72sinπ7=sinπ−sinπ72sinπ7=0−sinπ72sinπ7=−sinπ72sinπ7=−12
Jadi, nilai cos2π7+cos4π7+cos6π7=−12.♡
Nomor 12
Jika limx→a(f(x)+1g(x))=4 dan limx→a(f(x)−1g(x))=−3,
maka limx→a(f(x)g(x))=...
♠ Substitusi semua x dengan a pada masing-masing limit:
limx→a(f(x)+1g(x))=4⇒(f(a)+1g(a))=4 ...pers(i)
limx→a(f(x)−1g(x))=−3⇒(f(a)−1g(a))=−3 ...pers(ii)
♠ Eliminasi pers(i) dan pers(ii), diperoleh : f(a)=12,g(a)=27.
♠ Substitusi nilai f(a) dan g(a)
limx→a(f(x)g(x))=(f(a)g(a))=12×27=214
Jadi, nilai limx→a(f(x)g(x))=214.♡
limx→a(f(x)+1g(x))=4⇒(f(a)+1g(a))=4 ...pers(i)
limx→a(f(x)−1g(x))=−3⇒(f(a)−1g(a))=−3 ...pers(ii)
♠ Eliminasi pers(i) dan pers(ii), diperoleh : f(a)=12,g(a)=27.
♠ Substitusi nilai f(a) dan g(a)
limx→a(f(x)g(x))=(f(a)g(a))=12×27=214
Jadi, nilai limx→a(f(x)g(x))=214.♡
Nomor 13
Jika A=[1021], maka (I+A)5=....
♠ Konsep perpangkatan bentuk matriks tertentu
A=[10b1]→An=[10b1]n=[10b×n1]
matriks identitas : I=[1001]
♠ Menentukan hasil (I+A)5
(I+A)5=([1001]+[1021])5=([2022])5=(2[1011])5=25(1011)5=32(101×51)=32(1051)(I+A)5=(32016032)
Jadi, nilai (I+A)5=(32016032).♡
A=[10b1]→An=[10b1]n=[10b×n1]
matriks identitas : I=[1001]
♠ Menentukan hasil (I+A)5
(I+A)5=([1001]+[1021])5=([2022])5=(2[1011])5=25(1011)5=32(101×51)=32(1051)(I+A)5=(32016032)
Jadi, nilai (I+A)5=(32016032).♡
Nomor 14
Misalkan A(t) menyatakan luas daerah di bawah kurva y=bx2,0≤x≤t. Jika titik P(x0,0) sehingga A(x0):A(1)=1:8, maka perbandingan
luas trapesium ABPQ:DCPQ=...


♠ Menentukan A(t):
A(t)=∫t0bx2dx=[b3x3]t0=b3(t3−03)=b3t3t=x0→A(x0)=b3(x0)3t=1→A(1)=b3(1)3=b3
♠ Menentukan x0 dari A(x0):A(1)=1:8
A(x0)A(1)=18⇒b3(x0)3b3=18⇒x30=18⇒x0=12
♠ Menentukan titik A, Q, dan D dengan menggunakan y=bx2
titik A : x=−1⇒y=b(−1)2=b. Jadi titik A(-1, b)
titik Q : x=12⇒y=b(12)2=b. Jadi titik Q(1/2, b/4)
titik D : x=1⇒y=b(1)2=b. Jadi titik D(1, b)
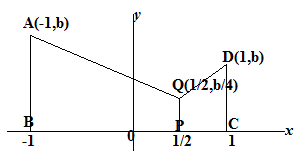
♠ Menentukan perbandingan luas ABPQ:DCPQ
L.ABPQL.DCPQ=12(AB+PQ).BP12(CD+PQ).CP=(b+b4).32(b+b4).12=31
Jadi, perbandingan luas L.ABPQL.DCPQ=31.♡
A(t)=∫t0bx2dx=[b3x3]t0=b3(t3−03)=b3t3t=x0→A(x0)=b3(x0)3t=1→A(1)=b3(1)3=b3
♠ Menentukan x0 dari A(x0):A(1)=1:8
A(x0)A(1)=18⇒b3(x0)3b3=18⇒x30=18⇒x0=12
♠ Menentukan titik A, Q, dan D dengan menggunakan y=bx2
titik A : x=−1⇒y=b(−1)2=b. Jadi titik A(-1, b)
titik Q : x=12⇒y=b(12)2=b. Jadi titik Q(1/2, b/4)
titik D : x=1⇒y=b(1)2=b. Jadi titik D(1, b)
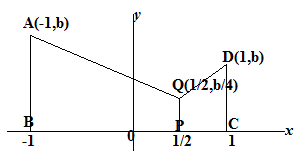
♠ Menentukan perbandingan luas ABPQ:DCPQ
L.ABPQL.DCPQ=12(AB+PQ).BP12(CD+PQ).CP=(b+b4).32(b+b4).12=31
Jadi, perbandingan luas L.ABPQL.DCPQ=31.♡
Nomor 15
Diberikan polinomial Q(x) dan f(x)=ax3+(a−b)x2+2bx+a. Jika Q(x)f(x) dan Q(x) berturut-turut
memberikan sisa -26 dan 1 apabila masing-masing dibagi x−2 ,dan f(x) habis dibagi x−1, maka f(x)
dibagi x2+x memberikan sisa ....
♠ Teorema sisa : f(x)x−a⇒sisa=f(a)
artinya : substitusi x=a ke f(x) dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
Q(x):(x−2), sisa = 1 , artinya Q(2)=1 ....pers(i)
Q(x)f(x):(x−2), sisa = -26 , artinya Q(2)f(2)=−26 ....pers(ii)
f(x):(x−1), sisa = 0 (karena habis dibagi) , artinya f(1)=0 ....pers(iii)
Substitusi Pers(i) ke pers(ii) diperoleh f(2)=−26 ....pers(iv)
♠ Menentukan fungsi f(x) dengan f(1)=0 dan f(2)=−26
x=2→f(x)=ax3+(a−b)x2+2bx+af(2)=a.23+(a−b).22+2b.2+a−26=8a+4a−4b+4b+a−26=13aa=−2x=1→f(x)=ax3+(a−b)x2+2bx+af(1)=a.13+(a−b).12+2b.1+a0=a+a−b+2b+ab=−3ab=−3(−2)=6
Sehingga fungsinya :
f(x)=ax3+(a−b)x2+2bx+a
f(x)=−2x3+(−2−6)x2+2.(6)x+(−2)
f(x)=−2x3−8x2+12x−2
f(0)=−2.03−8.02+12.0−2→f(0)=−2
f(−1)=−2.(−1)3−8.(−1)2+12.(−1)−2→f(−1)=−20
♠ Menentukan sisa pembagian dengan substitusi nilai x
f(x) dibagi x2+x=x(x+1) , misal sisanya S(x)=mx+n
x=0→ sisa =f(0)m.0+n=−2n=−2x=−1→ sisa =f(−1)m.(−1)+n=−20−m+(−2)=−20m=18
Sehingga sisanya : S(x)=mx+n=18x−2
Jadi, sisanya adalah 18x−2.♡
artinya : substitusi x=a ke f(x) dengan hasil sama dengan sisanya
Suatu fungsi habis dibagi, artinya sisanya = 0 .
Pembagian Polinomial :
Q(x):(x−2), sisa = 1 , artinya Q(2)=1 ....pers(i)
Q(x)f(x):(x−2), sisa = -26 , artinya Q(2)f(2)=−26 ....pers(ii)
f(x):(x−1), sisa = 0 (karena habis dibagi) , artinya f(1)=0 ....pers(iii)
Substitusi Pers(i) ke pers(ii) diperoleh f(2)=−26 ....pers(iv)
♠ Menentukan fungsi f(x) dengan f(1)=0 dan f(2)=−26
x=2→f(x)=ax3+(a−b)x2+2bx+af(2)=a.23+(a−b).22+2b.2+a−26=8a+4a−4b+4b+a−26=13aa=−2x=1→f(x)=ax3+(a−b)x2+2bx+af(1)=a.13+(a−b).12+2b.1+a0=a+a−b+2b+ab=−3ab=−3(−2)=6
Sehingga fungsinya :
f(x)=ax3+(a−b)x2+2bx+a
f(x)=−2x3+(−2−6)x2+2.(6)x+(−2)
f(x)=−2x3−8x2+12x−2
f(0)=−2.03−8.02+12.0−2→f(0)=−2
f(−1)=−2.(−1)3−8.(−1)2+12.(−1)−2→f(−1)=−20
♠ Menentukan sisa pembagian dengan substitusi nilai x
f(x) dibagi x2+x=x(x+1) , misal sisanya S(x)=mx+n
x=0→ sisa =f(0)m.0+n=−2n=−2x=−1→ sisa =f(−1)m.(−1)+n=−20−m+(−2)=−20m=18
Sehingga sisanya : S(x)=mx+n=18x−2
Jadi, sisanya adalah 18x−2.♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.