Pembahasan Soal UMPTN Matematika IPA tahun 2001 Nomor 6 sampai 10

Nomor 6

Garis

$g$ menghubungkan titik A(5,0) dan titik B(

$10 \cos \theta, 10 \sin \theta$ ). Titik P terletak pada AB sehingga AP:PB = 2:3. Jika

$\theta \,$ berubah dai

$0 \,$ sampai

$2\pi$ , maka titik P bergerak menelusuri kurva yang berupa .....

$\spadesuit \,$ Gambar

$\spadesuit \,$ Konsep Vektor

$AP:PB=m:n \rightarrow \vec{p} = \frac{m\vec{b} + n\vec{a}}{m+n}$

$\spadesuit \,$ Menentukan titik

$P(x,y)$

$\begin{align} AP : PB & = 2:3 \\ P(x,y) & = \frac{2\vec{b} + 3\vec{a}}{2+3} \\ & = \frac{2(10 \cos \theta, 10 \sin \theta ) + 3(5,0)}{5} \\ & = \frac{(20 \cos \theta, 20 \sin \theta ) + (15,0)}{5} \, \, \text{(bagi 5)} \\ & = (4 \cos \theta, 4 \sin \theta ) + (3,0) \\ P(x,y) & = (4 \cos \theta + 3, 4 \sin \theta ) \end{align}$
sehingga diperoleh :

$x = 4 \cos \theta + 3 \rightarrow \cos \theta = \frac{x-3}{4}$

$y = 4 \sin \theta \rightarrow \sin \theta = \frac{y}{4}$

$\spadesuit \,$ Konsep identitas trigonometri

$\begin{align} \cos ^2 \theta + \sin ^2 \theta & = 1 \\ \left( \frac{x-3}{4} \right)^2 + \left( \frac{y}{4} \right)^2 & = 1 \\ \frac{x^2-6x+9}{16} + \frac{y^2}{16} & = 1 \, \, \text{(kali 16)} \\ x^2-6x+9 + y^2 & = 16 \\ x^2 + y^2 -6x & = 7 \, \, \text{(berupa lingkaran)} \end{align}$
Jadi, kurvanya adalah

$x^2 + y^2 -6x = 7 . \heartsuit$

Nomor 7

Titik A dan B terletak pada elips

$16x^2+9y^2+64x-72y+64 = 0 \,$ . Jarak terbesar yang mungkin dari A ke B adalah .....

$\clubsuit \,$ Konsep dasar elips

$\frac{(x-m)^2}{a^2} + \frac{(y-n)^2}{b^2} = 1$
jika

$a > b, \,$ maka jarak terbesar =

$2a$
jika

$a < b, \,$ maka jarak terbesar =

$2b$

$\clubsuit \,$ Menyederhanakan bentuk elipsnya

$\begin{align} 16x^2+9y^2+64x-72y+64 & = 0 \\ 16(x^2 + 4x) + 9(y^2-8y) + 64 & = 0 \\ 16(x^2 + 4x + 4 - 4) + 9(y^2-8y+ 16 - 16) + 64 & = 0 \\ 16(x^2 + 4x + 4) - 16 . 4 + 9(y^2-8y+ 16 ) - 9 . 16 + 64 & = 0 \\ 16(x+2)^2 - 64 + 9(y-4)^2 - 144 + 64 & = 0 \\ 16(x+2)^2 + 9(y-4)^2 & = 144 \, \, \text{(bagi 144)} \\ \frac{(x+2)^2}{9} + \frac{(y-4)^2}{16} & = 1 \\ \frac{(x+2)^2}{3^2} + \frac{(y-4)^2}{4^2} & = 1 \end{align}$
Diperoleh :

$a = 3 , \,$ dan

$\, b = 4$
Titik A dan B terletak pada elips, sehingga
jarak terjauhnya adalah 2

$\times b$ = 2

$\times 4$ = 8
Jadi, jarak A dan B terjauhnya adalah 8.

$\heartsuit$

Nomor 8

Dari barisan empat buah bilangan, jumlah tiga bilangan pertama sama dengan nol dan kuadrat bilangan pertama sama dengan

$- \frac{2}{3} \,$ kali bilangan ketiga. Jika setiap dua bilangan yang berdekatan sama selisihnya, maka bilangan keempat adalah .....

$\spadesuit \,$ Dua bilangan berdekatan selisihnya sama, sehingga ini merupakan barisan aritmetika
Misal barisannya :

$a-b, \, a, \, a+b, \, a+2b$

$\spadesuit \,$ Jumlah tiga suku pertama = 0

$\begin{align} u_1 + u_2 + u_3 & = 0 \\ (a-b)+a+(a+b) & = 0 \\ 3a & = 0 \\ a & = 0 \end{align}$
Sehingga barisannya :

$-b, \, 0, \, b, \, 2b$

$\spadesuit \,$ Menentukan nilai

$b$

$\begin{align} u_1^2 & = -\frac{2}{3} (U_3) \\ (-b)^2 & = -\frac{2}{3} b \\ b^2 + \frac{2}{3}b & = 0 \\ b(b+\frac{2}{3}) & = 0 \\ b = 0 \vee b & = -\frac{2}{3} \end{align}$
yang memenuhi

$b = -\frac{2}{3} \,$ karena selisihnya tidak sama dengan nol.
Sehingga

$u_4 = 2b = 2 \times (-\frac{2}{3}) = -\frac{4}{3}$
Jadi, bilangan keempatnya adalah

$-\frac{4}{3} . \heartsuit$

Nomor 9

Panjang rusuk kubus ABCD.EFGH adalah

$a$ . Jarak A ke diagonal BH adalah ....

$\clubsuit \,$ Gambar

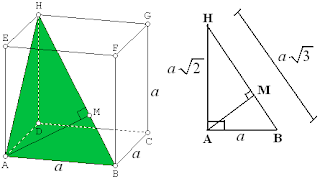
Jarak A ke BH adalah jarak A ke M (panjang AM)
AH = diagonal sisi =

$a\sqrt{2} \,$ dan BH = diagonal ruang =

$a\sqrt{3}$

$\clubsuit \,$ Menentukan AM

$\begin{align} Luas \, \Delta ABH \, \text{(alas AB)} \, & = Luas \, \Delta ABH \, \text{(alas BH)} \\ \frac{1}{2}. AB.AH & = \frac{1}{2}.BH.AM \\ a.a\sqrt{2} & = a\sqrt{3}.AM \\ AM & = \frac{a\sqrt{2}}{\sqrt{3}} \\ AM & = \frac{1}{3}a\sqrt{6} \end{align}$
Jadi, jaraknya adalah

$\frac{1}{3}a\sqrt{6} . \heartsuit$

Nomor 10

Kurva

$y = (x^2+2)^2 \,$ memotong sumbu Y di titik A. Persamaan garis singgung pada kurva tersebut di A adalah .....

$\spadesuit \,$ Menentukan titik potong sumbu Y, substitusi

$x = 0$

$\begin{align} y & = (x^2+2)^2 \\ y & = (0^2+2)^2 \\ y & = 4 \end{align}$
sehingga titik A(0,4)

$\spadesuit \,$ Menentukan gradien garis singgung di titik A(0,4) :

$m = f^\prime (0)$

$\begin{align} y & = (x^2+2)^2 \\ y^\prime & = 2(x^2+2).2x \\ y^\prime & = 4x(x^2+2) \\ m & = f^\prime (0) \\ m & = 4.0.(0^2+2) \\ m & = 0 \end{align}$

$\spadesuit \,$ Menentukan garis singgung di titik

$(x_1,y_1) = (0,4) \,$ dengan

$m = 0$