Nomor 6
Diketahui 4x2−2mx+2m−3=0 supaya kedua akar - akarnya real berbeda dan positif haruslah .....
♠ PK : 4x2−2mx+2m−3=0
→a=4,b=−2m,c=2m−3
♠ Syarat akar real beda positif
x1+x2>0,x1.x2>0,D>0
♠ Menyelesaikan syarat-syaratnya
*) x1+x2>0→−ba>0→−(−2m)4>0→m>0 ....(HP1)
*) x1.x2>0→ca>0→2m−34>0→m>32 ....(HP2)
*) syarat D>0
D>0b2−4ac>0(−2m)2−4.4.(2m−3)>04m2−32m+48>0(bagi 4)m2−8m+12>0(m−2)(m−6)>0m=2∨m=6

HP3 = {m<2∨m>6}
Sehingga HP = HP1∩HP2∩HP3={32<m<2∨m>6}
Jadi, solusinya HP={32<m<2∨m>6}.♡
→a=4,b=−2m,c=2m−3
♠ Syarat akar real beda positif
x1+x2>0,x1.x2>0,D>0
♠ Menyelesaikan syarat-syaratnya
*) x1+x2>0→−ba>0→−(−2m)4>0→m>0 ....(HP1)
*) x1.x2>0→ca>0→2m−34>0→m>32 ....(HP2)
*) syarat D>0
D>0b2−4ac>0(−2m)2−4.4.(2m−3)>04m2−32m+48>0(bagi 4)m2−8m+12>0(m−2)(m−6)>0m=2∨m=6

HP3 = {m<2∨m>6}
Sehingga HP = HP1∩HP2∩HP3={32<m<2∨m>6}
Jadi, solusinya HP={32<m<2∨m>6}.♡
Nomor 7
Himpunan penyelesaian pertaksamaan :
2log(x−2)≤log(2x−1) adalah .....
♣ Konsep dasar
alogb=c, syaratnya : a>0,a≠1,b>0
alogbn=n.alogb
alogf(x)≤alogg(x)→f(x)≤g(x), syaratnya a>1
♣ Menyelesaikan syarat logaritma
2log(x−2)≤log(2x−1)
Syarat :
x−2>0→x>2
2x−1>0→x>12
yang memenuhi kedua syarat adalah : HP1 = {x>2}
♣ Menyelesaikan pertidaksamaan
2log(x−2)≤log(2x−1)log(x−2)2≤log(2x−1)(coret log nya)(x−2)2≤(2x−1)(x−2)2≤(2x−1)x2−4x+4≤(2x−1)x2−4x+4−2x+1≤0x2−6x+5≤0(x−1)(x−5)≤0x=1∨x=5

HP2 = {1≤m≤5}
Sehingga HP=HP1∩HP2={2<m≤5}
Jadi, solusinya HP={2<m≤5}.♡
alogb=c, syaratnya : a>0,a≠1,b>0
alogbn=n.alogb
alogf(x)≤alogg(x)→f(x)≤g(x), syaratnya a>1
♣ Menyelesaikan syarat logaritma
2log(x−2)≤log(2x−1)
Syarat :
x−2>0→x>2
2x−1>0→x>12
yang memenuhi kedua syarat adalah : HP1 = {x>2}
♣ Menyelesaikan pertidaksamaan
2log(x−2)≤log(2x−1)log(x−2)2≤log(2x−1)(coret log nya)(x−2)2≤(2x−1)(x−2)2≤(2x−1)x2−4x+4≤(2x−1)x2−4x+4−2x+1≤0x2−6x+5≤0(x−1)(x−5)≤0x=1∨x=5

HP2 = {1≤m≤5}
Sehingga HP=HP1∩HP2={2<m≤5}
Jadi, solusinya HP={2<m≤5}.♡
Nomor 8
limx→07x2+sin(2x2)tan23x=......
♠ Konsep limit
limx→0axtanbx=ab dan limx→0sinaxtanbx=ab
♠ Menyelesaikan limitnya
limx→07x2+sin(2x2)tan23x=limx→07x2tan23x+sin(2x2)tan23x=732+232=79+29=99=1
Jadi, nilai limitnya adalah 1. ♡
limx→0axtanbx=ab dan limx→0sinaxtanbx=ab
♠ Menyelesaikan limitnya
limx→07x2+sin(2x2)tan23x=limx→07x2tan23x+sin(2x2)tan23x=732+232=79+29=99=1
Jadi, nilai limitnya adalah 1. ♡
Nomor 9
Himpunan penyelesaian pertaksamaan x2−|x|≤6 adalah .....
♣ Konsep Harga mutlak
|x|={x, untuk x≥0(atau)−x, untuk x<0
♣ penyelesaian dibagi menjadi dua kasus
*) untuk x≥0, maka |x|=x
x2−|x|≤6 (ganti |x|=x)x2−x≤6x2−x−6≤0(x+2)(x−3)≤0x=−2∨x=3
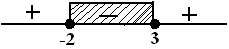
dari syarat x≥0, maka solusinya : HP1 = {0≤x≤3}
*) untuk x<0, maka |x|=−x
x2−|x|≤6 (ganti |x|=−x)x2−(−x)≤6x2+x−6≤0(x−2)(x+3)≤0x=2∨x=−3

dari syarat x<0, maka solusinya : HP2 = {−3≤x<0}
sehingga solusinya : HP = HP1∪HP2={−3≤x≤3}
Jadi, solusinya HP={−3≤x≤3}.♡
|x|={x, untuk x≥0(atau)−x, untuk x<0
♣ penyelesaian dibagi menjadi dua kasus
*) untuk x≥0, maka |x|=x
x2−|x|≤6 (ganti |x|=x)x2−x≤6x2−x−6≤0(x+2)(x−3)≤0x=−2∨x=3

dari syarat x≥0, maka solusinya : HP1 = {0≤x≤3}
*) untuk x<0, maka |x|=−x
x2−|x|≤6 (ganti |x|=−x)x2−(−x)≤6x2+x−6≤0(x−2)(x+3)≤0x=2∨x=−3

dari syarat x<0, maka solusinya : HP2 = {−3≤x<0}
sehingga solusinya : HP = HP1∪HP2={−3≤x≤3}
Jadi, solusinya HP={−3≤x≤3}.♡
Nomor 10
Titik P(a,b) dicerminkan terhadap sumbu X, bayangannya dicerminkan pula terhadap sumbu Y, maka bayangan terakhir titik P
merupakan ......
A. Pencerminan titik P terhadap garis y=x
B. Pencerminan titik P terhadap garis y=−x
C. Pencerminan titik P terhadap garis sumbu Y
D. Perputaran titik P dengan pusat titik O(0,0) sebesar π radian berlawanan perputaran jarum jam
E. Perputaran titik P dengan pusat titik O(0,0) sebesar π2 radian berlawanan perputaran jarum jam
A. Pencerminan titik P terhadap garis y=x
B. Pencerminan titik P terhadap garis y=−x
C. Pencerminan titik P terhadap garis sumbu Y
D. Perputaran titik P dengan pusat titik O(0,0) sebesar π radian berlawanan perputaran jarum jam
E. Perputaran titik P dengan pusat titik O(0,0) sebesar π2 radian berlawanan perputaran jarum jam
♠ Menentukan matriks gabungan
T1= (pencerminan sumbu X) =(100−1)
T2= (pencerminan sumbu Y) =(−1001)
Matriks gabungannya (MT) :
MT=T2.T1=(−1001)(100−1)=(−100−1)
♠ Matriks transformasi (−100−1) sama dengan matriks perputaran sebesar π berlawanan jarum jam
MT=(cosθ−sinθsinθcosθ)=(cosπ−sinπsinπcosπ)=(−100−1)
Jadi, solusinya opsi D. ♡
T1= (pencerminan sumbu X) =(100−1)
T2= (pencerminan sumbu Y) =(−1001)
Matriks gabungannya (MT) :
MT=T2.T1=(−1001)(100−1)=(−100−1)
♠ Matriks transformasi (−100−1) sama dengan matriks perputaran sebesar π berlawanan jarum jam
MT=(cosθ−sinθsinθcosθ)=(cosπ−sinπsinπcosπ)=(−100−1)
Jadi, solusinya opsi D. ♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.