Nomor 11
Jika 0≤x≤π , maka himpunan penyelesaian pertaksamaan cosx−sin2x<0 adalah ....
♣ Konsep Trigonometri : sin2x=2sinx.cosx
♣ Menyelesaikan soal
cosx−sin2x<0cosx−2sinx.cosx<0cosx(1−2sinx)<0cosx=0∨sinx=12cosx=0→x=π2,3π2sinx=12→x=π6,5π6
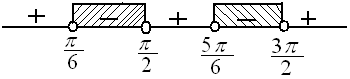
HP={π6<x<π2∪5π6<x<3π2}
Jadi, solusi yang memenuhi 0≤x≤π adalah
HP={π6<x<π2}∪{5π6<x≤π}.♡
♣ Menyelesaikan soal
cosx−sin2x<0cosx−2sinx.cosx<0cosx(1−2sinx)<0cosx=0∨sinx=12cosx=0→x=π2,3π2sinx=12→x=π6,5π6
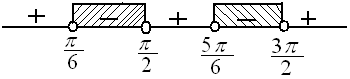
HP={π6<x<π2∪5π6<x<3π2}
Jadi, solusi yang memenuhi 0≤x≤π adalah
HP={π6<x<π2}∪{5π6<x≤π}.♡
Nomor 12
Syarat agar akar-akar persamaan kuadrat (p−2)x2+2px+p−1=0 negatif dan berlainan adalah ....
♠ PK : (p−2)x2+2px+p−1=0
→a=p−2,b=2p,c=p−1
♠ Syarat akar-akar negatif dan berlainan
x1+x2<0,x1.x2>0, dan D>0
♠ Menyelesaikan syarat-syaratnya
syarat I: x1+x2<0→−ba<0−2pp−2<0p=0∨p=2
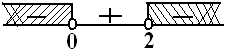
HP1={p<0∨p>2}
syarat II: x1.x2>0→ca>0p−1p−2>0p=1∨p=2
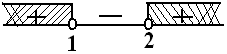
HP2={p<1∨p>2}
syarat III: D>0→b2−4ac>0(2p)2−4(p−2)(p−1)>04p2−4p2+12p−8>012p>8p>812=23HP3={p>23}
Sehingga solusinya :
HP=HP1∩HP2∩HP3={p>2}
Jadi, solusinya HP={p>2}.♡
→a=p−2,b=2p,c=p−1
♠ Syarat akar-akar negatif dan berlainan
x1+x2<0,x1.x2>0, dan D>0
♠ Menyelesaikan syarat-syaratnya
syarat I: x1+x2<0→−ba<0−2pp−2<0p=0∨p=2
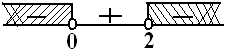
HP1={p<0∨p>2}
syarat II: x1.x2>0→ca>0p−1p−2>0p=1∨p=2
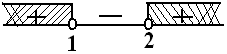
HP2={p<1∨p>2}
syarat III: D>0→b2−4ac>0(2p)2−4(p−2)(p−1)>04p2−4p2+12p−8>012p>8p>812=23HP3={p>23}
Sehingga solusinya :
HP=HP1∩HP2∩HP3={p>2}
Jadi, solusinya HP={p>2}.♡
Nomor 13
Melalui titik (1,−34) dibuat garis singgung pada parabola y=14x2 , absis kedua titik singgungnya adalah ....
♠ Misalkan persamaan garis singgungnya :
y=mx+b ....pers(i)
♠ Substitusi titik (1,−34) ke pers(i)
(1,−34)→y=mx+b−34=m.1+bb=−m−34
Sehingga garisnya menjadi :
y=mx+b→y=mx−m−34 ....pers(ii)
♠ Gradien garis singgung : m=f′(x)
y=14x2→y′=12x
sehingga : m=f′(x)→m=12x
♠ Substitusi m=12x ke pers(ii)
y=mx−m−34→y=12x.x−12x−34
y=12x2−12x−34 ....pers(iii)
♠ Karena bersinggungan, maka nilai parabola = garis
y1=y214x2=12x2−12x−34(kali 4)x2=2x2−2x−3x2−2x−3=0(x+1)(x−3)=0x=−1∨x=3
Jadi, absis titik singgungnya adalah x=−1 dan x=3.♡
y=mx+b ....pers(i)
♠ Substitusi titik (1,−34) ke pers(i)
(1,−34)→y=mx+b−34=m.1+bb=−m−34
Sehingga garisnya menjadi :
y=mx+b→y=mx−m−34 ....pers(ii)
♠ Gradien garis singgung : m=f′(x)
y=14x2→y′=12x
sehingga : m=f′(x)→m=12x
♠ Substitusi m=12x ke pers(ii)
y=mx−m−34→y=12x.x−12x−34
y=12x2−12x−34 ....pers(iii)
♠ Karena bersinggungan, maka nilai parabola = garis
y1=y214x2=12x2−12x−34(kali 4)x2=2x2−2x−3x2−2x−3=0(x+1)(x−3)=0x=−1∨x=3
Jadi, absis titik singgungnya adalah x=−1 dan x=3.♡
Cara II : Menentukan nilai m (gradiennya)
♠ Misalkan persamaan garis singgungnya :
y=mx+b ....pers(i)
♠ Substitusi titik (1,−34) ke pers(i)
(1,−34)→y=mx+b−34=m.1+bb=−m−34
Sehingga garisnya menjadi :
y=mx+b→y=mx−m−34 ....pers(ii)
♠ Syarat bersinggungan : D=0
y1=y214x2=mx−m−34(kali 4)x2=4mx−4m−3x2−4mx+4m+3=0D=0(syarat garis singgung)b2−4ac=0(−4m)2−4.1.(4m+3)=016m2−16m−12=04m2−4m−4=0(2m+1)(2m−3)=0m=−12∨m=32
♠ Gradien garis singgung : m=f′(x)
y=14x2→y′=12x
sehingga : m=f′(x)→m=12x
untuk m=−12→−12=12x→x=−1
untuk m=32→32=12x→x=3
Jadi, absis titik singgungnya adalah x=−1 dan x=3.♡
♠ Misalkan persamaan garis singgungnya :
y=mx+b ....pers(i)
♠ Substitusi titik (1,−34) ke pers(i)
(1,−34)→y=mx+b−34=m.1+bb=−m−34
Sehingga garisnya menjadi :
y=mx+b→y=mx−m−34 ....pers(ii)
♠ Syarat bersinggungan : D=0
y1=y214x2=mx−m−34(kali 4)x2=4mx−4m−3x2−4mx+4m+3=0D=0(syarat garis singgung)b2−4ac=0(−4m)2−4.1.(4m+3)=016m2−16m−12=04m2−4m−4=0(2m+1)(2m−3)=0m=−12∨m=32
♠ Gradien garis singgung : m=f′(x)
y=14x2→y′=12x
sehingga : m=f′(x)→m=12x
untuk m=−12→−12=12x→x=−1
untuk m=32→32=12x→x=3
Jadi, absis titik singgungnya adalah x=−1 dan x=3.♡
Nomor 14
Diketahui p(x)=ax5+bx−1 dengan a dan b adalah konstan. Jika p(x) dibagi (x−2006) bersisa 3, maka bila
p(x) dibagi dengan (x+2006) akan bersisa ....
♠ Teorema sisa : P(x)x+a→sisa=P(−a)
♠ Pembagian p(x)=ax5+bx−1 dibagi (x−2006),
dengan sisa = 3
p(x)x−2006→sisa=p(2006)→3=p(2006)
Diperoleh :
p(2006)=3→a(2006)5+b.(2006)−1=3a(2006)5+b(2006)=4...pers(i)
♠ Pembagian p(x)=ax5+bx−1 dibagi (x+2006)
p(x)x+2006→sisa=p(−2006)
Diperoleh :
sisa=p(−2006)=a(−2006)5+b(−2006)−1=−a(2006)5−b(2006)−1=−[a(2006)5+b(2006)]−1[dari pers(i)]=−[4]−1=−5
Jadi, sisa pembagiannya adalah -5. ♡
♠ Pembagian p(x)=ax5+bx−1 dibagi (x−2006),
dengan sisa = 3
p(x)x−2006→sisa=p(2006)→3=p(2006)
Diperoleh :
p(2006)=3→a(2006)5+b.(2006)−1=3a(2006)5+b(2006)=4...pers(i)
♠ Pembagian p(x)=ax5+bx−1 dibagi (x+2006)
p(x)x+2006→sisa=p(−2006)
Diperoleh :
sisa=p(−2006)=a(−2006)5+b(−2006)−1=−a(2006)5−b(2006)−1=−[a(2006)5+b(2006)]−1[dari pers(i)]=−[4]−1=−5
Jadi, sisa pembagiannya adalah -5. ♡
Nomor 15
Jika 8x2y=32 dan 4x.2y=322, maka x+y=....
♣ Sifat eksponen :
am.an=am+n,aman=am−n dan (am)n=amn
♣ Menyederhanakan soal
Persamaan pertama :
8x2y=32→(23)x2y=2523x2y=25→23x−y=253x−y=5...pers(i)
Persamaan kedua :
4x.2y=322→(22)x.2y=(25)222x2y=210→22x+y=2102x+y=10...pers(ii)
♣ Eliminasi pers(i) dan pers(ii)
3x−y=52x+y=10+5x=15x=3
pers(ii): 2x+y=10→2.3+y=10→y=4
Sehingga nilai x+y=3+4=7
Jadi, nilai x+y=7.♡
am.an=am+n,aman=am−n dan (am)n=amn
♣ Menyederhanakan soal
Persamaan pertama :
8x2y=32→(23)x2y=2523x2y=25→23x−y=253x−y=5...pers(i)
Persamaan kedua :
4x.2y=322→(22)x.2y=(25)222x2y=210→22x+y=2102x+y=10...pers(ii)
♣ Eliminasi pers(i) dan pers(ii)
3x−y=52x+y=10+5x=15x=3
pers(ii): 2x+y=10→2.3+y=10→y=4
Sehingga nilai x+y=3+4=7
Jadi, nilai x+y=7.♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.