Nomor 6
Diketahui f(x)=1−xx untuk setiap bilangan real x≠0. Jika g:R→R adalah
suatu fungsi sehingga (g∘f)(x)=2x+1, maka fungsi invers g−1(x)=....
♠ Menentukan komposisinya
(g∘f)(x)=2x+1g(f(x))=2x+1g(1−xx)=2x+1misaly=1−xx→x=1y+1g(1−xx)=2x+1g(y)=2.(1y+1)+1g(y)=y+3y+1g(x)=x+3x+1
♠ Menentukan inversnya
konsep : g(x)=ax+bcx+d→g−1(x)=dx−b−cx+a
sehingga invernya :
g(x)=x+3x+1→g−1(x)=x−3−x+1=x−31−x
Jadi, fungsi inversnya adalah g−1(x)=x−31−x.♡
(g∘f)(x)=2x+1g(f(x))=2x+1g(1−xx)=2x+1misaly=1−xx→x=1y+1g(1−xx)=2x+1g(y)=2.(1y+1)+1g(y)=y+3y+1g(x)=x+3x+1
♠ Menentukan inversnya
konsep : g(x)=ax+bcx+d→g−1(x)=dx−b−cx+a
sehingga invernya :
g(x)=x+3x+1→g−1(x)=x−3−x+1=x−31−x
Jadi, fungsi inversnya adalah g−1(x)=x−31−x.♡
Nomor 7
Jika garis singgung di titik (1,2) pada parabola y=ax2+bx+4 memiliki persamaan y=−6x+8, maka nilai a dan b
berturut-turut adalah ....
♣ Substitusi titik singgung ke parabolanya
(1,2)→y=ax2+bx+42=ax.12+b.1+4a+b=−2...pesr(i)
♣ Menentukan turunan dan gradien garis singgung
y=ax2+bx+4→y′=2ax+b
y=−6x+8→m=−6
gradien garis singgung di titik (1,2)
m=f′(1)−6=2a.1+b2a+b=−6...pesr(ii)
♣ Eliminasi pers(i) dan pers(ii)
2a+b=−6a+b=−2−a=−4
pers(i) : a+b=−2→−4+b=−2→b=2
Jadi, nilai a=−4 dan b=2.♡
(1,2)→y=ax2+bx+42=ax.12+b.1+4a+b=−2...pesr(i)
♣ Menentukan turunan dan gradien garis singgung
y=ax2+bx+4→y′=2ax+b
y=−6x+8→m=−6
gradien garis singgung di titik (1,2)
m=f′(1)−6=2a.1+b2a+b=−6...pesr(ii)
♣ Eliminasi pers(i) dan pers(ii)
2a+b=−6a+b=−2−a=−4
pers(i) : a+b=−2→−4+b=−2→b=2
Jadi, nilai a=−4 dan b=2.♡
Nomor 8
Luas daerah dibatasi oleh grafik fungsi-fungsi y=sinx,y=cosx dan sumbu X untuk 0≤x≤π2 adalah ....
♠ Gambar
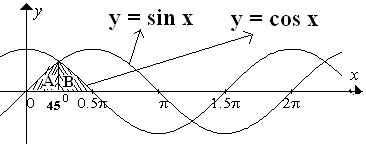
♠ Menentukan luas arsiran
Larsir=LA+LB=45∘∫0sinxdx+90∘∫45∘cosxdx=−[cosx]45∘0+[sinx]90∘45∘=−[cos45∘−cos0]+[sin90∘−sin45∘]=−[12√2−1]+[1−12√2]=2−√2
Jadi, luas daerahnya adalah 2−√2.♡

♠ Menentukan luas arsiran
Larsir=LA+LB=45∘∫0sinxdx+90∘∫45∘cosxdx=−[cosx]45∘0+[sinx]90∘45∘=−[cos45∘−cos0]+[sin90∘−sin45∘]=−[12√2−1]+[1−12√2]=2−√2
Jadi, luas daerahnya adalah 2−√2.♡
Nomor 9
Dalam suatu ujian, perbandingan banyaknya peserta pria dan wanita adalah 6:5. Diketahui 3 peserta pria dan 1 peserta wanita tidak lulus.
Jika perbandingan jumlah peserta pria dan wanita yang lulus ujian adalah 9:8, maka jumlah peserta yang lulus adalah ....
♣ Misal : P = siswa pria, W = siswa wanita
Perbandingan 6 : 5
PW=65→P=65W ....pers(i)
♣ 3 pria dan 1 wanita tidak lulus
P−3W−1=98→8P=9W+15 ....pers(ii)
♣ Substitusi pers(i) ke pers(ii)
8P=9W+158(65W)=9W+15(kali 5)48W=45W+753W=75→W=25
pers(i): P=65W=65.25=30
Sehingga yang lulus = 30 + 25 - 4 = 51
Jadi, jumlah peserta yang lulus ada 51 orang. ♡
Perbandingan 6 : 5
PW=65→P=65W ....pers(i)
♣ 3 pria dan 1 wanita tidak lulus
P−3W−1=98→8P=9W+15 ....pers(ii)
♣ Substitusi pers(i) ke pers(ii)
8P=9W+158(65W)=9W+15(kali 5)48W=45W+753W=75→W=25
pers(i): P=65W=65.25=30
Sehingga yang lulus = 30 + 25 - 4 = 51
Jadi, jumlah peserta yang lulus ada 51 orang. ♡
Nomor 10
Diketahui 0≤a≤π2 dan 0≤b≤π2 . Jika sina−sinb=35
dan cosa+cosb=45, maka sin(a+b)=....
♠ Rumus dasar trigonometri
identitas : sin2a+cos2a=1 dan sin2b+cos2b=1
Jumlah sudut : cos(a+b)=cosacosb−sinasinb
♠ Kuadratkan kedua persamaan
(sina−sinb)2=(35)2sin2a+sin2b−2sinasinb=925(cosa+cosb)2=(45)2cos2a+cos2b+2cosacosb=1625
Jumlahkan kedua persamaan :
sin2a+sin2b−2sinasinb=925cos2a+cos2b+2cosacosb=1625+
(sin2a+cos2a)+(sin2b+cos2b)+2(cosacosb−sinasinb)=925+16251+1+2cos(a+b)=1cos(a+b)=−12
Buat segitiga :

Sehingga, nilai sin(a+b)=12√3
Jadi, nilai sin(a+b)=12√3.♡
identitas : sin2a+cos2a=1 dan sin2b+cos2b=1
Jumlah sudut : cos(a+b)=cosacosb−sinasinb
♠ Kuadratkan kedua persamaan
(sina−sinb)2=(35)2sin2a+sin2b−2sinasinb=925(cosa+cosb)2=(45)2cos2a+cos2b+2cosacosb=1625
Jumlahkan kedua persamaan :
sin2a+sin2b−2sinasinb=925cos2a+cos2b+2cosacosb=1625+
(sin2a+cos2a)+(sin2b+cos2b)+2(cosacosb−sinasinb)=925+16251+1+2cos(a+b)=1cos(a+b)=−12
Buat segitiga :

Sehingga, nilai sin(a+b)=12√3
Jadi, nilai sin(a+b)=12√3.♡
Pak Putu itu no. 6 kan di soal fog(x)=2x+1
BalasHapustapi bapak cari nya gof(x)=2x+1 hehe
Hallow @Bobbi,
HapusTerimakasih untuk koreksinya.
Setelah saya cek lagi soal aslinya, ternyata salah ketik. Dan sudah saya perbaiki.
Bagi Bobbi dan pembaca lainnya juga, jiga ada koreksi untuk pembahasannya, mohon untuk share di kolom komentar ya, sehingga bisa kita cek dan perbaiki lagi, agar isi pembahasan di blog dunia-informa ini semakin berkualitas.
Begitu juga kalau ada alternatif solusi yang lainnya.
Terimakasih juga untuk kunjungannya ke blog dunia-informa ini.
semoga terus bisa membantu.
Semangat belajarnya.