Nomor 11
Diketahui f(x)=−2x2−(p+1)x+2p. Fungsi f(x) mempunyai nilai maksimum 8. Jika p bernilai p1
atau p2. Nilai p1+p2 adalah ....
♠ FK : f(x)=−2x2−(p+1)x+2p
→a=−2,b=−(p+1),c=2p
♠ Nilai maksimum FK (yp) dengan rumus yp=D−4a
♠ Menentukan nilai p dengan yp=8
yp=8D−4a=8b2−4ac−4a=8[−(p+1)]2−4.(−2).(2p)−4.(−2)=8p2+2p+1+16p8=8p2+18p+1=64p2+18p−63=0
PK : p2+18p−63=0, akar-akarnya p1 dan p2
Sehingga : p1+p2=−ba=−181=−18
Jadi, nilai p1+p2=−18.♡
→a=−2,b=−(p+1),c=2p
♠ Nilai maksimum FK (yp) dengan rumus yp=D−4a
♠ Menentukan nilai p dengan yp=8
yp=8D−4a=8b2−4ac−4a=8[−(p+1)]2−4.(−2).(2p)−4.(−2)=8p2+2p+1+16p8=8p2+18p+1=64p2+18p−63=0
PK : p2+18p−63=0, akar-akarnya p1 dan p2
Sehingga : p1+p2=−ba=−181=−18
Jadi, nilai p1+p2=−18.♡
Nomor 12
Integral yang menyatakan luas daerah di kuadran pertama yang dibatasi oleh kurva y=1x , garis y=x,
garis x=2, dan sumbu X adalah ....
♣ Gambar

♣ Menentukan luas arsir
Larsir=LA+LBLarsir=1∫0xdx+2∫11xdx
Jadi, luasnya adalah 1∫0xdx+2∫11xdx.♡

♣ Menentukan luas arsir
Larsir=LA+LBLarsir=1∫0xdx+2∫11xdx
Jadi, luasnya adalah 1∫0xdx+2∫11xdx.♡
Nomor 13
Satu dari dua persamaan garis singgung dari lingkaran x2+y2−2x−4y=0 yang tegak lurus terhadap garis
x−2y+4=0 adalah ....
♠ Menentukan pusat dan jari-jari lingkaran
x2+y2−2x−4y=0→A=−2,B=−4,C=0
Pusat (a,b) dengan a=−A2=−−22=1 dan b=−B2=−−42=2
Sehingga pusatnya : (a,b)=(1,2)
jari-jari : r=√a2+b2−C=√12+22−0=√5
♠ Menentukan gradien garis singgungnya
x−2y+4=0→m1=−xy=−1−2=12
Garis singgung tegak lurus, maka gradiennya :
m.m1=−1→m=−1m1=−112=−2
♠ Menentukan persamaan garis singgung lingkaran
y−b=m(x−a)±r√1+m2y−2=−2(x−1)±√5√1+(−2)2y−2=−2x+1±√5√5y−2=−2x+1±5(i).y−2=−2x+1+5→y+2x−9=0(atau)(ii).y−2=−2x+1−5→y+2x+1=0
Jadi, persamaan garis singgungnya adalah
y+2x−9=0∨y+2x+1=0.♡
x2+y2−2x−4y=0→A=−2,B=−4,C=0
Pusat (a,b) dengan a=−A2=−−22=1 dan b=−B2=−−42=2
Sehingga pusatnya : (a,b)=(1,2)
jari-jari : r=√a2+b2−C=√12+22−0=√5
♠ Menentukan gradien garis singgungnya
x−2y+4=0→m1=−xy=−1−2=12
Garis singgung tegak lurus, maka gradiennya :
m.m1=−1→m=−1m1=−112=−2
♠ Menentukan persamaan garis singgung lingkaran
y−b=m(x−a)±r√1+m2y−2=−2(x−1)±√5√1+(−2)2y−2=−2x+1±√5√5y−2=−2x+1±5(i).y−2=−2x+1+5→y+2x−9=0(atau)(ii).y−2=−2x+1−5→y+2x+1=0
Jadi, persamaan garis singgungnya adalah
y+2x−9=0∨y+2x+1=0.♡
Nomor 14
Rata-rata nilai ujian matematika dari 30 siswa adalah 88. Jika rata-rata nilai ujian itu untuk semua anak laki-laki
dan semua anak perempuan berturut-turut adalah 85 dan 90, maka banyaknya anak laki-laki adalah ....
♣ Misal :
¯xgb=88→ rata - rata gabungan
¯xp=90→ rata - rata perempuan
¯xl=85→ rata - rata laki - laki
Misal, banyak anak laki nl , maka banyak anak perempuan np=30−nl
♣ Menentukan nl dengan rata - rata gabungan
¯xgb=np.¯xp+nl.¯xlnp+nl88=(30−nl).90+nl.85(30−nl)+nl88=(30−nl).90+85nl3088.30=30.90−nl.90+85nl88.30=30.90−5nl5nl=30.90−88.305nl=30.2nl=30.25=12
Jadi, banyaknya anak laki - laki ada 12 siswa. ♡
¯xgb=88→ rata - rata gabungan
¯xp=90→ rata - rata perempuan
¯xl=85→ rata - rata laki - laki
Misal, banyak anak laki nl , maka banyak anak perempuan np=30−nl
♣ Menentukan nl dengan rata - rata gabungan
¯xgb=np.¯xp+nl.¯xlnp+nl88=(30−nl).90+nl.85(30−nl)+nl88=(30−nl).90+85nl3088.30=30.90−nl.90+85nl88.30=30.90−5nl5nl=30.90−88.305nl=30.2nl=30.25=12
Jadi, banyaknya anak laki - laki ada 12 siswa. ♡
Nomor 15
Diketahui sebelas orang duduk mengelilingi meja. Jika tiga orang tertentu harus duduk berdampingan, banyak cara kesebelas
orang tersebut dapat duduk adalah ....
♣ Gambar
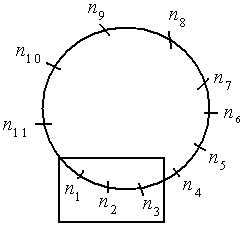
♣ Agar 3 orang selalu bersama, kita blok tiga orang tersebut (seperti gambar) dan dianggap menjadi satu orang , sehingga sekarang toal ada 9 orang duduk melingkar dengan cara duduk = (9 - 1)! = 8!
♣ Dari tiga orang yang diblok tadi ada 3! susunan
sehingga total cara = 3!.8!
Jadi, total cara duduk ada 3!.8! susunan. ♡

♣ Agar 3 orang selalu bersama, kita blok tiga orang tersebut (seperti gambar) dan dianggap menjadi satu orang , sehingga sekarang toal ada 9 orang duduk melingkar dengan cara duduk = (9 - 1)! = 8!
♣ Dari tiga orang yang diblok tadi ada 3! susunan
sehingga total cara = 3!.8!
Jadi, total cara duduk ada 3!.8! susunan. ♡
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.