Nomor 1
Tiga pria dan empat wanita akan duduk dalam satu baris. Banyak cara mereka duduk sehingga yang berjenis kelamin sama tidak berdampingan adalah ...
♣ Agar berjenis kelamin sama tidak berdampingan, maka susunan yang mungkin:
pada posisi pertama ada 4 pilihan wanita
pada posisi ketiga ada 3 pilihan wanita
pada posisi kelima ada 2 pilihan wanita
pada posisi ketujuh ada 1 pilihan wanita
pada posisi kedua ada 3 pilihan pria
pada posisi keempat ada 2 pilihan pria
pada posisi keenam ada 1 pilihan pria
dengan banyak cara :
=4.3.3.2.2.1.1=144 cara.
Jadi, total cara ada 144 susunan. ♡
| W | P | W | P | W | P | W |
pada posisi ketiga ada 3 pilihan wanita
pada posisi kelima ada 2 pilihan wanita
pada posisi ketujuh ada 1 pilihan wanita
pada posisi kedua ada 3 pilihan pria
pada posisi keempat ada 2 pilihan pria
pada posisi keenam ada 1 pilihan pria
dengan banyak cara :
| 4 | 3 | 3 | 2 | 2 | 1 | 1 |
Jadi, total cara ada 144 susunan. ♡
Nomor 2
Untuk setiap bilangan asli n didefinisikan matriks An=(n2n3n4n) Jika det(A1+A2+...+Ak)=−4050 ,
maka det(A2k)=...
An=(n2n3n4n) , Misalkan :p=1+2+3+...+k
A1+A2+...+Ak=(12.13.14.1)+(22.23.24.2)+...+(k2.k3.k4.k)=((1+2+...+k)2(1+2+...+k)3(1+2+...+k)4(1+2+...+k))=(p2p3p4p)det(A1+A2+...+Ak)=det(p2p3p4p)=4p2−6p2=−2p2det(A1+A2+...+Ak)=−4050−2p2=−4050p=45
♠ Menentukan nilai k :
p=45 dan Sn=n2(u1+un)
p=451+2+3+...+k=45k2(1+k)=45k2+k−9=0(k−9)(k+10)=0k=9atauk=−10yang memenuhi adalah x=9
♠ Menentukan nilai det(A2k) :
A2k=A2.9=A18=(182.183.184.18)
det(A2k)=det(A18)=det(182.183.184.18)=−648
Jadi determinan matriks A2k adalah -648 . ♡
A1+A2+...+Ak=(12.13.14.1)+(22.23.24.2)+...+(k2.k3.k4.k)=((1+2+...+k)2(1+2+...+k)3(1+2+...+k)4(1+2+...+k))=(p2p3p4p)det(A1+A2+...+Ak)=det(p2p3p4p)=4p2−6p2=−2p2det(A1+A2+...+Ak)=−4050−2p2=−4050p=45
♠ Menentukan nilai k :
p=45 dan Sn=n2(u1+un)
p=451+2+3+...+k=45k2(1+k)=45k2+k−9=0(k−9)(k+10)=0k=9atauk=−10yang memenuhi adalah x=9
♠ Menentukan nilai det(A2k) :
A2k=A2.9=A18=(182.183.184.18)
det(A2k)=det(A18)=det(182.183.184.18)=−648
Jadi determinan matriks A2k adalah -648 . ♡
Nomor 3
Diketahui persamaan x2+px+q=0 mempunyai akar-akar positif x1 dan x2 . Jika x1 , 6, x2 adalah tiga suku pertama barisan
geometri dan x1 , x2 , 14 tiga suku pertama barisan aritmatika, maka p+q=...
x2+px+q=0 memiliki akar-akar positif x1 dan x2
x1+x2=−ba⇒x1+x2=−p1=−p pers(i)
x1.x2=ca⇒x1.x2=q1=q pers(ii)
♣x1,6,x2 barisan geometri (rasionya sama) :
6x1=x26⇔x1.x2=36pers (iii)⇔q=36
♣x1,x2,14 barisan aritmatika (bedanya sama) :
x2−x1=14−x2⇔x1=2x2−14pers (iv)
♣ Substitusikan pers(iv) ke pers(iii) :
x1.x2=36(2x2−14)x2=36x22−7x2−18=0(x2−9)(x2+2)=0x2=9ataux2=−2yang memenuhi adalah x2=9
pers(iv) : x1=2x2−14⇔x1=2.9−14⇔x1=4
pers(i) : x1+x2=−p⇔4+9=−p⇔p=−13
Jadi, nilai p+q=−13+36=23.♡
x1+x2=−ba⇒x1+x2=−p1=−p pers(i)
x1.x2=ca⇒x1.x2=q1=q pers(ii)
♣x1,6,x2 barisan geometri (rasionya sama) :
6x1=x26⇔x1.x2=36pers (iii)⇔q=36
♣x1,x2,14 barisan aritmatika (bedanya sama) :
x2−x1=14−x2⇔x1=2x2−14pers (iv)
♣ Substitusikan pers(iv) ke pers(iii) :
x1.x2=36(2x2−14)x2=36x22−7x2−18=0(x2−9)(x2+2)=0x2=9ataux2=−2yang memenuhi adalah x2=9
pers(iv) : x1=2x2−14⇔x1=2.9−14⇔x1=4
pers(i) : x1+x2=−p⇔4+9=−p⇔p=−13
Jadi, nilai p+q=−13+36=23.♡
Nomor 4
Jika f(x)=(sinx+cosx)(cos2x+sin2x) dan f′(x)=2cos3x+g(x) maka g(x)=...
♠ Rumus perkalian:
sinxcosy=12(sin(x+y)+sin(x−y)),cosxsiny=12(sin(x+y)−sin(x−y)),sinxsiny=−12(cos(x+y)−cos(x−y)),cosxcosy=12(cos(x+y)+cos(x−y))
♠ Menyederhanakan fungsi f(x):
f(x)=(sinx+cosx)(cos2x+sin2x)=cos2xsinx+sin2xsinx+cos2xcosx+sin2xcox=12(sin3x−sinx)−12(cos3x−cosx)+12(cos3x+cosx)+12(sin3x+sinx)f(x)=sin3x+cosxf′(x)=3cos3x−sinx
♠ Menentukan fungsi g(x):
f′(x)=2cos3x+g(x)g(x)=f′(x)−2cos3xg(x)=(3cos3x−sinx)−2cos3xg(x)=cos3x−sinx
Jadi, Nilai g(x)=cos3x−sinx♡
sinxcosy=12(sin(x+y)+sin(x−y)),cosxsiny=12(sin(x+y)−sin(x−y)),sinxsiny=−12(cos(x+y)−cos(x−y)),cosxcosy=12(cos(x+y)+cos(x−y))
♠ Menyederhanakan fungsi f(x):
f(x)=(sinx+cosx)(cos2x+sin2x)=cos2xsinx+sin2xsinx+cos2xcosx+sin2xcox=12(sin3x−sinx)−12(cos3x−cosx)+12(cos3x+cosx)+12(sin3x+sinx)f(x)=sin3x+cosxf′(x)=3cos3x−sinx
♠ Menentukan fungsi g(x):
f′(x)=2cos3x+g(x)g(x)=f′(x)−2cos3xg(x)=(3cos3x−sinx)−2cos3xg(x)=cos3x−sinx
Jadi, Nilai g(x)=cos3x−sinx♡
Nomor 5
Diketahui D1 adalah daerah di kuadran I yang dibatasi oleh parabola y=94x2 , parabola y=x2 , dan
garis x=2 , dan D2 daerah yang dibatasi oleh garis x=2 , garis y=9 ,
dan parabola y=x2 . Jika luas D1=a , maka luas D2 adalah ...
♣ Luas D1 : (LD1=a)
LD1=∫20(94x2−x2)=∫20(54x2)=103LD1=a⇔a=103
♣ Luas D2 :
LD2=∫32(9−x2)=83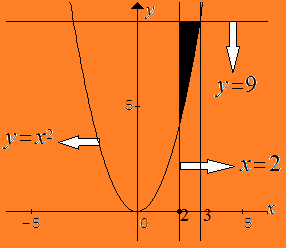
Sehingga LD2=83.1010=810.103=810a.
Jadi, LD2=810a♡
LD1=∫20(94x2−x2)=∫20(54x2)=103LD1=a⇔a=103

♣ Luas D2 :
LD2=∫32(9−x2)=83

Sehingga LD2=83.1010=810.103=810a.
Jadi, LD2=810a♡



Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.