Nomor 6
Diberikan limas T.ABC. Misalkan u=→TA,v=→TB,w=→TC. Jika P titik berat ΔABC, maka →TP=...
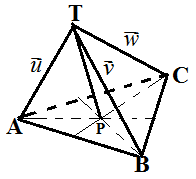

♠ Titik P adalah titik berat, sehingga:
→AP=23→AD dan →BD:→DC=1:1
♠ Menentukan vektor →TD dari gambar berikut:
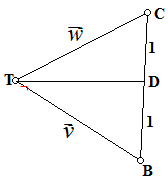
→TD=1.→v+1.→w1+1=→v+→w2
♠ Menentukan vektor →AD dan →AP :
→AD=→AT+→TD=−→u+(→v+→w2)→AD=→v+→w−2→u2→AP=23→AD→AP=23.(→v+→w−2→u2)→AP=13(→v+→w−2→u)
♠ Menentukan vektor →TP :
→TP=→TA+→AP=→u+13(→v+→w−2→u)=13(→u+→v+→w)
Jadi, →TP=13(→u+→v+→w).♡
→AP=23→AD dan →BD:→DC=1:1
♠ Menentukan vektor →TD dari gambar berikut:

→TD=1.→v+1.→w1+1=→v+→w2
♠ Menentukan vektor →AD dan →AP :
→AD=→AT+→TD=−→u+(→v+→w2)→AD=→v+→w−2→u2→AP=23→AD→AP=23.(→v+→w−2→u2)→AP=13(→v+→w−2→u)
♠ Menentukan vektor →TP :
→TP=→TA+→AP=→u+13(→v+→w−2→u)=13(→u+→v+→w)
Jadi, →TP=13(→u+→v+→w).♡
Nomor 7
Diketahui suatu parabola simetris terhadap garis x=−2, dan garis singgung parabola tersebut di titik (0, 1) sejajar garis 4x+y=4.
Titik puncak parabola tersebut adalah ...
♣ Misalkan persamaan fungsinya , y=f(x)=ax2+bx+c. Dengan titik puncak (xp,yp) :
xp=−b2a dan yp=f(xp) , serta f′(x)=2ax+b.
♣ Sumbu simetrinya x=−2 dengan x=xp :
x=xp⇔−2=−b2a⇔b=4a ...pers(i)
♣ Garis singgung di (0,1) , artinya titik (0,1) dilalui parabola, substitusi (0,1) ke persamaan parabola:
y=ax2+bx+c⇔1=a.02+b.0+c⇔c=1
sehingga persamaan parabolanya menjadi : f(x)=ax2+bx+1
♣ Gradien garis singgung sejajar dengan garis 4x+y=4, artinya gradiennya sama dengan gradien garis 4x+y=4 yaitu m=−4.
♣ Menentukan gradien garis singgung di titik (0,1):
m=f′(x)⇔−4=f′(0)⇔−4=2a.0+b⇔b=−4.
Pers(i) : b=4a⇔−4=4a⇔a=−1 .
Persamaan parabolanya menjadi : f(x)=−x2−4x+1
♣ Menentukan titik puncak:
xp=−2⇒yp=f(xp)=f(−2)=−(−2)2−4.(−2)+1=5.
Jadi, titik puncaknya adalah (xp,yp)=(−2,5).♡
♣ Sumbu simetrinya x=−2 dengan x=xp :
x=xp⇔−2=−b2a⇔b=4a ...pers(i)
♣ Garis singgung di (0,1) , artinya titik (0,1) dilalui parabola, substitusi (0,1) ke persamaan parabola:
y=ax2+bx+c⇔1=a.02+b.0+c⇔c=1
sehingga persamaan parabolanya menjadi : f(x)=ax2+bx+1
♣ Gradien garis singgung sejajar dengan garis 4x+y=4, artinya gradiennya sama dengan gradien garis 4x+y=4 yaitu m=−4.
♣ Menentukan gradien garis singgung di titik (0,1):
m=f′(x)⇔−4=f′(0)⇔−4=2a.0+b⇔b=−4.
Pers(i) : b=4a⇔−4=4a⇔a=−1 .
Persamaan parabolanya menjadi : f(x)=−x2−4x+1
♣ Menentukan titik puncak:
xp=−2⇒yp=f(xp)=f(−2)=−(−2)2−4.(−2)+1=5.
Jadi, titik puncaknya adalah (xp,yp)=(−2,5).♡
Nomor 8
Semua nilai a sehingga f(x)=log(4x+a.2x+a+3) selalu bernilai real adalah ...
♠ Syarat kogaritma : alogb syaratnya a>0,a≠1,b>0.
♠ Bentuk ax2+bx+c>0 adalah definit positif, syaratnya : a>0 dan D<0.
♠f(x)=log(4x+a.2x+a+3) syaratnya ;
4x+a.2x+a+3>0⇔(2x)2+a.2x+(a+3)>0 ⇔(p)2+ap+(a+3)>0 dengan p=2x>0
♠ Bentuk (p)2+ap+(a+3)>0 termasuk definit positif dengan a=1,b=a,c=a+3, syaratnya:
a=1>0(benar)D<0⇔b2−4ac<0a2−4.1.(a+3)<0a2−4a−12<0(a+2)(a−6)<0a=−2ataua=6

HP1={−2<a<6}
♠ Nilai p=2x selalu positif , sehingga untuk a positif maka nilai (p)2+ap+(a+3) juga positif . HP2={a≥0}
Jadi, HP=HP1∪HP2={a>−2}.♡
♠ Bentuk ax2+bx+c>0 adalah definit positif, syaratnya : a>0 dan D<0.
♠f(x)=log(4x+a.2x+a+3) syaratnya ;
4x+a.2x+a+3>0⇔(2x)2+a.2x+(a+3)>0 ⇔(p)2+ap+(a+3)>0 dengan p=2x>0
♠ Bentuk (p)2+ap+(a+3)>0 termasuk definit positif dengan a=1,b=a,c=a+3, syaratnya:
a=1>0(benar)D<0⇔b2−4ac<0a2−4.1.(a+3)<0a2−4a−12<0(a+2)(a−6)<0a=−2ataua=6

HP1={−2<a<6}
♠ Nilai p=2x selalu positif , sehingga untuk a positif maka nilai (p)2+ap+(a+3) juga positif . HP2={a≥0}
Jadi, HP=HP1∪HP2={a>−2}.♡
Nomor 9
Misalkan diberikan titik A(1, 0) dan B(0, 1) . Jika P bersifat |→PA|:|→PB|=√m:√n , maka P terletak pada
lingkaran dengan persamaan ...
♣ Misalkan titik P(x,y), panjang →PA dan →PB :
|→PA|=√(x−1)2+(y−0)2=√(x−1)2+y2
|→PB|=√(x−0)2+(y−1)2=√x2+(y−1)2
♣ Kuadratkan bentuk |→PA|:|→PB|=√m:√n
|→PA|:|→PB|=√m:√n(|→PA||→PB|)2=(√m√n)2(√(x−1)2+y2√x2+(y−1)2)2=(√m√n)2((x−1)2+y2x2+(y−1)2)=(mn)n[x2+y2+1−2x]=m[x2+y2+1−2y]n(x2+y2+1)−n.2x=m(x2+y2+1)−m.2yn(x2+y2+1)−m(x2+y2+1)=2nx−2my(n−m)(x2+y2+1)=2(nx−my)
Jadi, persamaan lingkarannya: (n−m)(x2+y2+1)=2(nx−my)♡
|→PA|=√(x−1)2+(y−0)2=√(x−1)2+y2
|→PB|=√(x−0)2+(y−1)2=√x2+(y−1)2
♣ Kuadratkan bentuk |→PA|:|→PB|=√m:√n
|→PA|:|→PB|=√m:√n(|→PA||→PB|)2=(√m√n)2(√(x−1)2+y2√x2+(y−1)2)2=(√m√n)2((x−1)2+y2x2+(y−1)2)=(mn)n[x2+y2+1−2x]=m[x2+y2+1−2y]n(x2+y2+1)−n.2x=m(x2+y2+1)−m.2yn(x2+y2+1)−m(x2+y2+1)=2nx−2my(n−m)(x2+y2+1)=2(nx−my)
Jadi, persamaan lingkarannya: (n−m)(x2+y2+1)=2(nx−my)♡
Nomor 10
Diketahui a,a+b, dan a+5b merupakan 3 suku pertama suatu barisan geometri. Jika a,a+b,x,y, dan z merupakan 5 suku pertama
suatu barisan aritmetika dan x+y+z=−15, maka suku ke-10 barisan aritmetika tersebut adalah ...
♠ Barisan geometri (rasio sama): a,a+b,a+5b
u2u1=u3u2⇔(u2)2=u1.u3⇔(a+b)2=a.(a+5b)
⇔b2−3ab=0⇔b(b−3a)=0
⇔b=0(tidak memenuhi)ataub=3a...pers(i)(memenuhi)
♠ Barisan aritmetika (beda/selisih sama): a,a+b,x,y, dan z
y−x=z−y⇔x+z=2y...pers(ii)
♠ Substitusi pers(ii) ke x+y+z=−15
x+y+z=−15⇔(x+z)+y=−15⇔2y+y=−15⇔y=−5
♠y adalah suku ke-4 pada barisan aritmatika, sehingga u4=−5
u4=−5⇔a+3b=−5⇔a+3(3a)=−5⇔a=−12
Pers(i) : b=3a⇔b=3.−12⇔b=−32
♠ Menentukan u10 pada barisan aritmatika :
u10=a+9b=−12+9.(−32)u10=−282=−14
Jadi, suku ke-10 : u10=−14.♡
u2u1=u3u2⇔(u2)2=u1.u3⇔(a+b)2=a.(a+5b)
⇔b2−3ab=0⇔b(b−3a)=0
⇔b=0(tidak memenuhi)ataub=3a...pers(i)(memenuhi)
♠ Barisan aritmetika (beda/selisih sama): a,a+b,x,y, dan z
y−x=z−y⇔x+z=2y...pers(ii)
♠ Substitusi pers(ii) ke x+y+z=−15
x+y+z=−15⇔(x+z)+y=−15⇔2y+y=−15⇔y=−5
♠y adalah suku ke-4 pada barisan aritmatika, sehingga u4=−5
u4=−5⇔a+3b=−5⇔a+3(3a)=−5⇔a=−12
Pers(i) : b=3a⇔b=3.−12⇔b=−32
♠ Menentukan u10 pada barisan aritmatika :
u10=a+9b=−12+9.(−32)u10=−282=−14
Jadi, suku ke-10 : u10=−14.♡


kok sulit to mas ,bikin yang sederhana bisa nggak ?
BalasHapus