Nomor 6
Persamaan kuadrat 2x2−px+1=0 dengan p>0 , mempunyai akar-akar α dan β. Jika x2−5x+q=0 mempunyai akar-akar
1α2 dan 1β2, maka q−p=...
♠ pk1 2x2−px+1=0 mempunyai akar-akar α dan β :
α+β=−ba=p2 dan α.β=ca=12
♠ pk2 x2−5x+q=0 mempunyai akar-akar x1=1α2 dan x2=1β2 :
x1+x2=−ba=51 dan x1.x2=ca=q1=q
♠ menentukan nilai p dan q dari pk2 dan pk1
x1.x2=1α2.1β2⇒q=1(α.β)2⇒q=1(12)2⇒q=4x1+x2=1α2+1β2⇒5=(α+β)2−2αβ(α.β)2⇒5=(p2)2−2.12(12)2⇒5=p2−4⇒p=±3
Karena p>0, maka nilai p=3 yang memenuhi , sehingga q−p=4−3=1 .
Jadi, nilai q−p=1.♡
α+β=−ba=p2 dan α.β=ca=12
♠ pk2 x2−5x+q=0 mempunyai akar-akar x1=1α2 dan x2=1β2 :
x1+x2=−ba=51 dan x1.x2=ca=q1=q
♠ menentukan nilai p dan q dari pk2 dan pk1
x1.x2=1α2.1β2⇒q=1(α.β)2⇒q=1(12)2⇒q=4x1+x2=1α2+1β2⇒5=(α+β)2−2αβ(α.β)2⇒5=(p2)2−2.12(12)2⇒5=p2−4⇒p=±3
Karena p>0, maka nilai p=3 yang memenuhi , sehingga q−p=4−3=1 .
Jadi, nilai q−p=1.♡
Nomor 7
Diketahui f(0)=1 dan f′(0)=2. Jika g(x)=1(2f(x)−1)3 , maka g′(0)=...
Nomor 8
Jika x1 dan x2 adalah penyelesaian persamaan (2logx)2+2logx=6, maka x1x2=...
Nomor 9
Diketahui matriks A=(12−12−12x). Jika |A|
menyatakan determinan A , maka deret geometri |A|+|A|2+|A|3+... konvergen ke ...
♣ Menentukan determinan A :
|A|=12x−(−12).(−12)⇒|A|=12x−14.
♣ Deret geometri tak hingga : s∞=a1−r dengan −1<r<1
♣ Deret |A|+|A|2+|A|3+... memiliki a=|A| dan r=u2u1=|A|2|A|=|A|
♣ Menentukan jumlah |A|+|A|2+|A|3+...
|A|+|A|2+|A|3+...=s∞=a1−r=|A|1−|A|=12x−141−(12x−14)=12x−141−(12x−14).44=2x−14−2x+1=2x−15−2x=−2x−12x−5
♣ Menentukan syarat rasio : −1<r<1
−1<r<1−1<|A|<1−1<12x−14<1(kali 4)−4<2x−1<4(ditambah 1)−3<2x<5(dibagi 2)−32<x<52
Jadi, |A|+|A|2+|A|3+...=−2x−12x−5 dengan −32<x<52.♡
|A|=12x−(−12).(−12)⇒|A|=12x−14.
♣ Deret geometri tak hingga : s∞=a1−r dengan −1<r<1
♣ Deret |A|+|A|2+|A|3+... memiliki a=|A| dan r=u2u1=|A|2|A|=|A|
♣ Menentukan jumlah |A|+|A|2+|A|3+...
|A|+|A|2+|A|3+...=s∞=a1−r=|A|1−|A|=12x−141−(12x−14)=12x−141−(12x−14).44=2x−14−2x+1=2x−15−2x=−2x−12x−5
♣ Menentukan syarat rasio : −1<r<1
−1<r<1−1<|A|<1−1<12x−14<1(kali 4)−4<2x−1<4(ditambah 1)−3<2x<5(dibagi 2)−32<x<52
Jadi, |A|+|A|2+|A|3+...=−2x−12x−5 dengan −32<x<52.♡
Nomor 10
Jika titik (x,y) memenuhi x2≤y≤x+6, maka nilai maksimum x+y adalah ...
♠x2≤y≤x+6 dapat dipecah menjadi y≤x+6 dan y≥x2
♠ Menentukan titik potong kedua kurva :
y1=y2x2=x+6x2−x−6=0(x+2)(x−3)=0x=−2ataux=3x=−2⇒y=(−2)2=4,titiknya:(−2,4)x=3⇒y=(3)2=9,titiknya:(3,9)
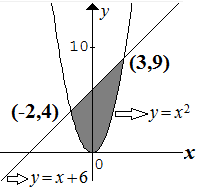
♠ Menentukan nilai maksimum dari x+y diperoleh di titik (3,9):
x+y=3+9=12
Jadi, nilai maksimum dari x+y adalah 12. ♡
♠ Menentukan titik potong kedua kurva :
y1=y2x2=x+6x2−x−6=0(x+2)(x−3)=0x=−2ataux=3x=−2⇒y=(−2)2=4,titiknya:(−2,4)x=3⇒y=(3)2=9,titiknya:(3,9)
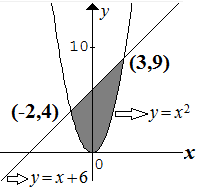
♠ Menentukan nilai maksimum dari x+y diperoleh di titik (3,9):
x+y=3+9=12
Jadi, nilai maksimum dari x+y adalah 12. ♡


Boleh minta file lengkapnya nggk Pak. Mkasih ya atas kesdiaannya.
BalasHapusHallow Leon.
HapusMaksudnya file yang mana mau diminta?
Ijin save
BalasHapusHallow @Yoga,
HapusSilahkan di save untuk dibaca secara offline ya.
Terima kasih untuk kunjungannya ke blog dunia informa ini.
Semoga terus bisa membantu.