Nomor 11
Jika untuk $ 0 \leq \alpha , \beta \leq \pi, \, $ berlaku
$ \sqrt{3} \tan \alpha \tan \beta = \tan \alpha - \tan \beta - \sqrt{3} \, $ dan
$ \sin \alpha \sin \beta = \frac{3}{4}, \, $ maka $ \cos (\alpha + \beta ) = .... $
$ \sqrt{3} \tan \alpha \tan \beta = \tan \alpha - \tan \beta - \sqrt{3} \, $ dan
$ \sin \alpha \sin \beta = \frac{3}{4}, \, $ maka $ \cos (\alpha + \beta ) = .... $
$\clubsuit \, $ Konsep trigonometri
$ \tan (x - y) = \frac{\tan x - \tan y}{1 + \tan x \tan y} $
$ \cos ( x- y ) = \cos x \cos y + \sin x \sin y $
$ \cos ( x + y ) = \cos x \cos y - \sin x \sin y $
$\clubsuit \, $ Menentukan nilai $ (\alpha - \beta ) $
$\begin{align} \sqrt{3} \tan \alpha \tan \beta & = \tan \alpha - \tan \beta - \sqrt{3} \\ \sqrt{3} + \sqrt{3} \tan \alpha \tan \beta & = \tan \alpha - \tan \beta \\ \sqrt{3} ( 1 + \tan \alpha \tan \beta ) & = \tan \alpha - \tan \beta \\ \frac{\tan \alpha - \tan \beta }{ 1 + \tan \alpha \tan \beta} & = \sqrt{3} \\ \tan ( \alpha - \beta ) & = \sqrt{3} \\ \alpha - \beta & = 60^\circ \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos \alpha \cos \beta $ dengan $ \sin \alpha \sin \beta = \frac{3}{4} $
$\begin{align} \alpha - \beta & = 60^\circ \\ \cos ( \alpha - \beta ) & = \cos ( 60^\circ ) \\ \cos \alpha \cos \beta + \sin \alpha \sin \beta & = \frac{1}{2} \\ \cos \alpha \cos \beta + \frac{3}{4} & = \frac{1}{2} \\ \cos \alpha \cos \beta & = -\frac{1}{4} \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos (\alpha + \beta ) $
$\begin{align} \cos ( \alpha + \beta ) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \cos ( \alpha + \beta ) & = -\frac{1}{4} - \frac{3}{4} \\ \cos ( \alpha + \beta ) & = -\frac{4}{4} = -1 \end{align}$
Jadi, nilai $ \cos (\alpha + \beta ) = - 1 . \heartsuit $
$ \tan (x - y) = \frac{\tan x - \tan y}{1 + \tan x \tan y} $
$ \cos ( x- y ) = \cos x \cos y + \sin x \sin y $
$ \cos ( x + y ) = \cos x \cos y - \sin x \sin y $
$\clubsuit \, $ Menentukan nilai $ (\alpha - \beta ) $
$\begin{align} \sqrt{3} \tan \alpha \tan \beta & = \tan \alpha - \tan \beta - \sqrt{3} \\ \sqrt{3} + \sqrt{3} \tan \alpha \tan \beta & = \tan \alpha - \tan \beta \\ \sqrt{3} ( 1 + \tan \alpha \tan \beta ) & = \tan \alpha - \tan \beta \\ \frac{\tan \alpha - \tan \beta }{ 1 + \tan \alpha \tan \beta} & = \sqrt{3} \\ \tan ( \alpha - \beta ) & = \sqrt{3} \\ \alpha - \beta & = 60^\circ \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos \alpha \cos \beta $ dengan $ \sin \alpha \sin \beta = \frac{3}{4} $
$\begin{align} \alpha - \beta & = 60^\circ \\ \cos ( \alpha - \beta ) & = \cos ( 60^\circ ) \\ \cos \alpha \cos \beta + \sin \alpha \sin \beta & = \frac{1}{2} \\ \cos \alpha \cos \beta + \frac{3}{4} & = \frac{1}{2} \\ \cos \alpha \cos \beta & = -\frac{1}{4} \end{align}$
$\clubsuit \, $ Menentukan nilai $ \cos (\alpha + \beta ) $
$\begin{align} \cos ( \alpha + \beta ) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \cos ( \alpha + \beta ) & = -\frac{1}{4} - \frac{3}{4} \\ \cos ( \alpha + \beta ) & = -\frac{4}{4} = -1 \end{align}$
Jadi, nilai $ \cos (\alpha + \beta ) = - 1 . \heartsuit $
Nomor 12
Persamaan lingkaran dengan titik pusat berada pada parabola $ y = x^2 \, $ dan menyinggung sumbu X adalah .....
$\spadesuit \, $ Misal pusat lingkarannya ($a,b$). Substitusi ke parabola $ y = x^2 \, $ (karena pusat terletak pada parabola)
$\begin{align} (a,b) \rightarrow y & = x^2 \\ b & = a^2 \end{align}$
Sehingga titik pusatnya ($a,b$) = ($a,a^2$)
$\spadesuit \, $ Lingkaran menyinggung sumbu X, maka jari-jarinya adalah $ b $
Sehingga : $ r = b = a^2 $
$\spadesuit \, $ Persamaan lingkaran dengan pusat ($a,b$) = ($a,a^2$) dengan jari - jari $ r = a^2 $
$\begin{align} (x-a)^2 + (y-b)^2 & = r^2 \\ (x-a)^2 + (y - a^2)^2 & = (a^2)^2 \\ x^2 - 2ax + a^2 + y^2 - 2a^2y + a^4 & = a^4 \\ x^2 + y^2 - 2ax - 2a^2 y + a^2 & = 0 \end{align}$
Jadi, persamaan lingkarannya $ x^2 + y^2 - 2ax - 2a^2 y + a^2 = 0 . \heartsuit $
$\begin{align} (a,b) \rightarrow y & = x^2 \\ b & = a^2 \end{align}$
Sehingga titik pusatnya ($a,b$) = ($a,a^2$)
$\spadesuit \, $ Lingkaran menyinggung sumbu X, maka jari-jarinya adalah $ b $
Sehingga : $ r = b = a^2 $
$\spadesuit \, $ Persamaan lingkaran dengan pusat ($a,b$) = ($a,a^2$) dengan jari - jari $ r = a^2 $
$\begin{align} (x-a)^2 + (y-b)^2 & = r^2 \\ (x-a)^2 + (y - a^2)^2 & = (a^2)^2 \\ x^2 - 2ax + a^2 + y^2 - 2a^2y + a^4 & = a^4 \\ x^2 + y^2 - 2ax - 2a^2 y + a^2 & = 0 \end{align}$
Jadi, persamaan lingkarannya $ x^2 + y^2 - 2ax - 2a^2 y + a^2 = 0 . \heartsuit $
Nomor 13
Jika $ \displaystyle \lim_{ x \to 0 } \frac{\sqrt{a + x} - \sqrt{a - x}}{x} = b $ .
Maka $ \displaystyle \lim_{ x \to 0 } \frac{\sqrt{b + x} - \sqrt{b - x}}{x} = .... $
Maka $ \displaystyle \lim_{ x \to 0 } \frac{\sqrt{b + x} - \sqrt{b - x}}{x} = .... $
$\spadesuit \, $ Penerapan L'Hospital pada limit
$ \displaystyle \lim_{ x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \, $ solusinya : $ \displaystyle \lim_{ x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{ x \to k } \frac{f^\prime (x)}{g^\prime (x)} $
diturunkan sampai bentuknya tidak $ \frac{0}{0} \, $ lagi.
$\spadesuit \, $ Menentukan hubungan $ b $ dan $ \, a $ dengan turunan
$\begin{align} \displaystyle \lim_{ x \to 0 } \frac{\sqrt{a + x} - \sqrt{a - x}}{x} & = b \, \, \text{(turunan)} \\ \displaystyle \lim_{ x \to 0 } \frac{ \frac{1}{2\sqrt{a + x}} - \frac{-1}{2\sqrt{a - x}}}{1} & = b \\ \frac{ \frac{1}{2\sqrt{a + 0}} - \frac{-1}{2\sqrt{a - 0}}}{1} & = b \\ \frac{1}{2\sqrt{a}} + \frac{1}{2\sqrt{a}} & = b \\ \frac{2}{2\sqrt{a}} & = b \\ b & = \frac{1}{\sqrt{a}} \end{align}$
$\spadesuit \, $ Menyelesaikan soal dengan turunan dan $ b = \frac{1}{\sqrt{a}} $
$\begin{align} \displaystyle \lim_{ x \to 0 } \frac{\sqrt{b + x} - \sqrt{b - x}}{x} & = \displaystyle \lim_{ x \to 0 } \frac{ \frac{1}{2\sqrt{b + x}} - \frac{-1}{2\sqrt{b - x}}}{1} \\ & = \frac{ \frac{1}{2\sqrt{b + 0}} - \frac{-1}{2\sqrt{b - 0}}}{1} \\ & = \frac{1}{2\sqrt{b}} + \frac{1}{2\sqrt{b}} \\ & = \frac{2}{2\sqrt{b}} = \frac{1}{\sqrt{b}} \\ & = \frac{1}{\sqrt{\frac{1}{\sqrt{a}}}} = \frac{1}{ \frac{ \sqrt{1}}{\sqrt{\sqrt{a}}} } \\ & = \frac{1}{ \frac{ 1}{\sqrt{\sqrt{a}}} } \\ & = \sqrt{\sqrt{a}} \end{align}$
Jadi, hasil limitnya adalah $ \sqrt{\sqrt{a}} . \heartsuit $
$ \displaystyle \lim_{ x \to k } \frac{f(x)}{g(x)} = \frac{0}{0} \, $ solusinya : $ \displaystyle \lim_{ x \to k } \frac{f(x)}{g(x)} = \displaystyle \lim_{ x \to k } \frac{f^\prime (x)}{g^\prime (x)} $
diturunkan sampai bentuknya tidak $ \frac{0}{0} \, $ lagi.
$\spadesuit \, $ Menentukan hubungan $ b $ dan $ \, a $ dengan turunan
$\begin{align} \displaystyle \lim_{ x \to 0 } \frac{\sqrt{a + x} - \sqrt{a - x}}{x} & = b \, \, \text{(turunan)} \\ \displaystyle \lim_{ x \to 0 } \frac{ \frac{1}{2\sqrt{a + x}} - \frac{-1}{2\sqrt{a - x}}}{1} & = b \\ \frac{ \frac{1}{2\sqrt{a + 0}} - \frac{-1}{2\sqrt{a - 0}}}{1} & = b \\ \frac{1}{2\sqrt{a}} + \frac{1}{2\sqrt{a}} & = b \\ \frac{2}{2\sqrt{a}} & = b \\ b & = \frac{1}{\sqrt{a}} \end{align}$
$\spadesuit \, $ Menyelesaikan soal dengan turunan dan $ b = \frac{1}{\sqrt{a}} $
$\begin{align} \displaystyle \lim_{ x \to 0 } \frac{\sqrt{b + x} - \sqrt{b - x}}{x} & = \displaystyle \lim_{ x \to 0 } \frac{ \frac{1}{2\sqrt{b + x}} - \frac{-1}{2\sqrt{b - x}}}{1} \\ & = \frac{ \frac{1}{2\sqrt{b + 0}} - \frac{-1}{2\sqrt{b - 0}}}{1} \\ & = \frac{1}{2\sqrt{b}} + \frac{1}{2\sqrt{b}} \\ & = \frac{2}{2\sqrt{b}} = \frac{1}{\sqrt{b}} \\ & = \frac{1}{\sqrt{\frac{1}{\sqrt{a}}}} = \frac{1}{ \frac{ \sqrt{1}}{\sqrt{\sqrt{a}}} } \\ & = \frac{1}{ \frac{ 1}{\sqrt{\sqrt{a}}} } \\ & = \sqrt{\sqrt{a}} \end{align}$
Jadi, hasil limitnya adalah $ \sqrt{\sqrt{a}} . \heartsuit $
Nomor 14
Bila panjang proyeksi vektor $ \vec{b} = \vec{i} - 2 \vec{j} \, $ pada vektor $ \vec{a} = x\vec{i} + y \vec{j} \, $ dengan
$ x, y > 0 \, $ adalah 1, maka nilai $ 4x-3y+1 = .... $
$\spadesuit \, $ Konsep dasar : Panjang proyeksi $ \vec{b} \, $ pada $ \, \vec{a} $
Panjang = $ \frac{\vec{b}.\vec{a}}{|\vec{a}| } $
$\spadesuit \, $ Menentukan $ \vec{a}.\vec{b} \, $ dan $ |\vec{a}| $
$ \vec{b} = \vec{i} - 2 \vec{j} \, $ dan $ \, \vec{a} = x\vec{i} + y \vec{j} $
$ \vec{a} . \vec{b} = (x . 1) + y. (-2) = x - 2y $
$ |\vec{a}| = \sqrt{x^2 + y^2 } $
$\spadesuit \, $ Menentukan hubungan $ x \, $ dan $ \, y \, $ dengan panjang proyeksi 1
$\begin{align} \text{Panjang} & = \frac{\vec{b}.\vec{a}}{|\vec{a}|} \\ 1 & = \frac{x - 2y}{\sqrt{x^2 + y^2 }} \\ \sqrt{x^2 + y^2 } & = x - 2y \, \, \text{(kuadratkan kedua ruas)} \\ x^2 + y^2 & = x^2 - 4xy + 4y^2 \\ 3y^2 - 4xy & = 0 \\ y(3y-4x) & = 0 \\ y = 0 \vee 3y-4x & = 0 \rightarrow y = \frac{4x}{3} \end{align}$
Karena $ y \, $ positif, maka nilai yang memenuhi adalah $ y = \frac{4x}{3} $
Sehingga nilai $ 4x-3y+1 $
$\begin{align} 4x-3y+1 & = 4x-3(\frac{4x}{3}) +1 \\ & = 4x - 4x + 1 \\ & = 1 \end{align}$
Jadi, nilai $ 4x-3y+1 = 1 . \heartsuit $
Panjang = $ \frac{\vec{b}.\vec{a}}{|\vec{a}| } $
$\spadesuit \, $ Menentukan $ \vec{a}.\vec{b} \, $ dan $ |\vec{a}| $
$ \vec{b} = \vec{i} - 2 \vec{j} \, $ dan $ \, \vec{a} = x\vec{i} + y \vec{j} $
$ \vec{a} . \vec{b} = (x . 1) + y. (-2) = x - 2y $
$ |\vec{a}| = \sqrt{x^2 + y^2 } $
$\spadesuit \, $ Menentukan hubungan $ x \, $ dan $ \, y \, $ dengan panjang proyeksi 1
$\begin{align} \text{Panjang} & = \frac{\vec{b}.\vec{a}}{|\vec{a}|} \\ 1 & = \frac{x - 2y}{\sqrt{x^2 + y^2 }} \\ \sqrt{x^2 + y^2 } & = x - 2y \, \, \text{(kuadratkan kedua ruas)} \\ x^2 + y^2 & = x^2 - 4xy + 4y^2 \\ 3y^2 - 4xy & = 0 \\ y(3y-4x) & = 0 \\ y = 0 \vee 3y-4x & = 0 \rightarrow y = \frac{4x}{3} \end{align}$
Karena $ y \, $ positif, maka nilai yang memenuhi adalah $ y = \frac{4x}{3} $
Sehingga nilai $ 4x-3y+1 $
$\begin{align} 4x-3y+1 & = 4x-3(\frac{4x}{3}) +1 \\ & = 4x - 4x + 1 \\ & = 1 \end{align}$
Jadi, nilai $ 4x-3y+1 = 1 . \heartsuit $
Nomor 15
$ u(x) \, $ dan $ v(x) \, $ masing - masing merupakan fungsi dengan grafik seperti pada gambar di bawah ini.

Jika $ f(x) = u(x) . v(x) , \, $ maka $ f^\prime (1) = .... $

Jika $ f(x) = u(x) . v(x) , \, $ maka $ f^\prime (1) = .... $
$\clubsuit \, $ Grafik fungsi sekitar $ x = 1 $
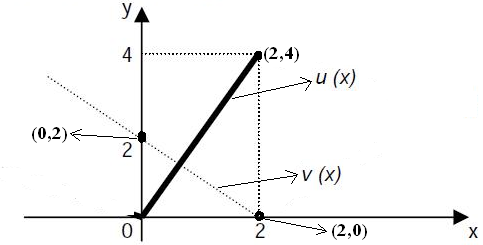
$\clubsuit \, $ Grafik fungsi sekitar $ x = 1 $ membentuk garis lurus, sehingga persamaannya menggunakan rumus garis lurus
Persamaan garis melalui dua titik ($x_1,y_1$) dan ($x_2,y_2$)
$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $
$\clubsuit \, $ Fungsi $ u(x) \, $ melalui titik (0,0) dan (2,4)
$\begin{align} \frac{y - y_1}{y_2 - y_1} & = \frac{x - x_1}{x_2 - x_1} \\ \frac{y - 0}{4-0} & = \frac{x - 0}{2-0} \\ \frac{y }{4} & = \frac{x }{2} \\ y & = 2x \end{align}$
Sehingga : $ u(x) = 2x $
$\clubsuit \, $ Fungsi $ v(x) \, $ melalui titik (2,0) dan (0,2)
$\begin{align} \frac{y - y_1}{y_2 - y_1} & = \frac{x - x_1}{x_2 - x_1} \\ \frac{y - 0}{2-0} & = \frac{x - 2}{0-2} \\ \frac{y }{2} & = \frac{x - 2}{ -2} \\ y & = -x + 2 \end{align}$
Sehingga : $ v(x) = -x + 2 $
$\clubsuit \, $ Menentukan $ f(x) \, $ dan turunannya
$\begin{align} f(x) & = u(x) v(x) \\ f(x) & = (2x) (-x+2) \\ f(x) & = -2x^2 + 4x \\ f^\prime (x) & = -4x + 4 \\ x = 1 \rightarrow f^\prime (1) & = -4.1 + 4 = 0 \end{align}$
Jadi, nilai $ f^\prime (1) = 0 . \heartsuit $

$\clubsuit \, $ Grafik fungsi sekitar $ x = 1 $ membentuk garis lurus, sehingga persamaannya menggunakan rumus garis lurus
Persamaan garis melalui dua titik ($x_1,y_1$) dan ($x_2,y_2$)
$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $
$\clubsuit \, $ Fungsi $ u(x) \, $ melalui titik (0,0) dan (2,4)
$\begin{align} \frac{y - y_1}{y_2 - y_1} & = \frac{x - x_1}{x_2 - x_1} \\ \frac{y - 0}{4-0} & = \frac{x - 0}{2-0} \\ \frac{y }{4} & = \frac{x }{2} \\ y & = 2x \end{align}$
Sehingga : $ u(x) = 2x $
$\clubsuit \, $ Fungsi $ v(x) \, $ melalui titik (2,0) dan (0,2)
$\begin{align} \frac{y - y_1}{y_2 - y_1} & = \frac{x - x_1}{x_2 - x_1} \\ \frac{y - 0}{2-0} & = \frac{x - 2}{0-2} \\ \frac{y }{2} & = \frac{x - 2}{ -2} \\ y & = -x + 2 \end{align}$
Sehingga : $ v(x) = -x + 2 $
$\clubsuit \, $ Menentukan $ f(x) \, $ dan turunannya
$\begin{align} f(x) & = u(x) v(x) \\ f(x) & = (2x) (-x+2) \\ f(x) & = -2x^2 + 4x \\ f^\prime (x) & = -4x + 4 \\ x = 1 \rightarrow f^\prime (1) & = -4.1 + 4 = 0 \end{align}$
Jadi, nilai $ f^\prime (1) = 0 . \heartsuit $

